Delta-Sigma Modulator (3) — MASH & HK-MASH & SP-MASH

几种 DSM 结构

传统的 MASH 结构

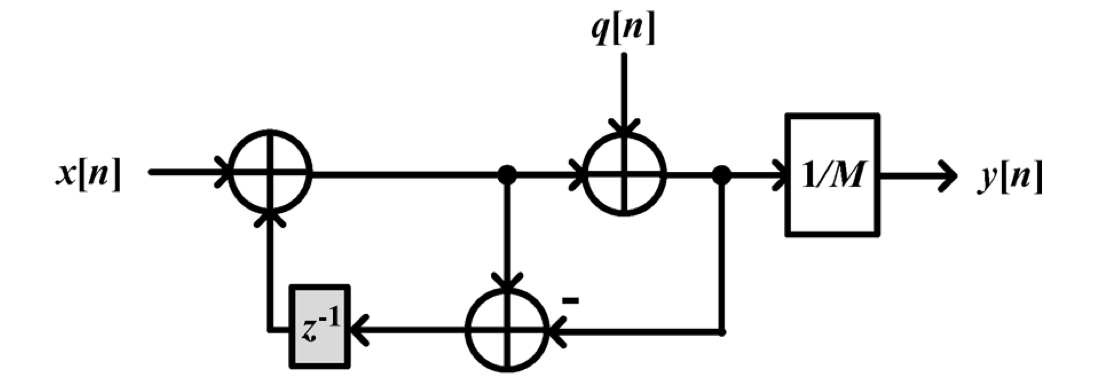
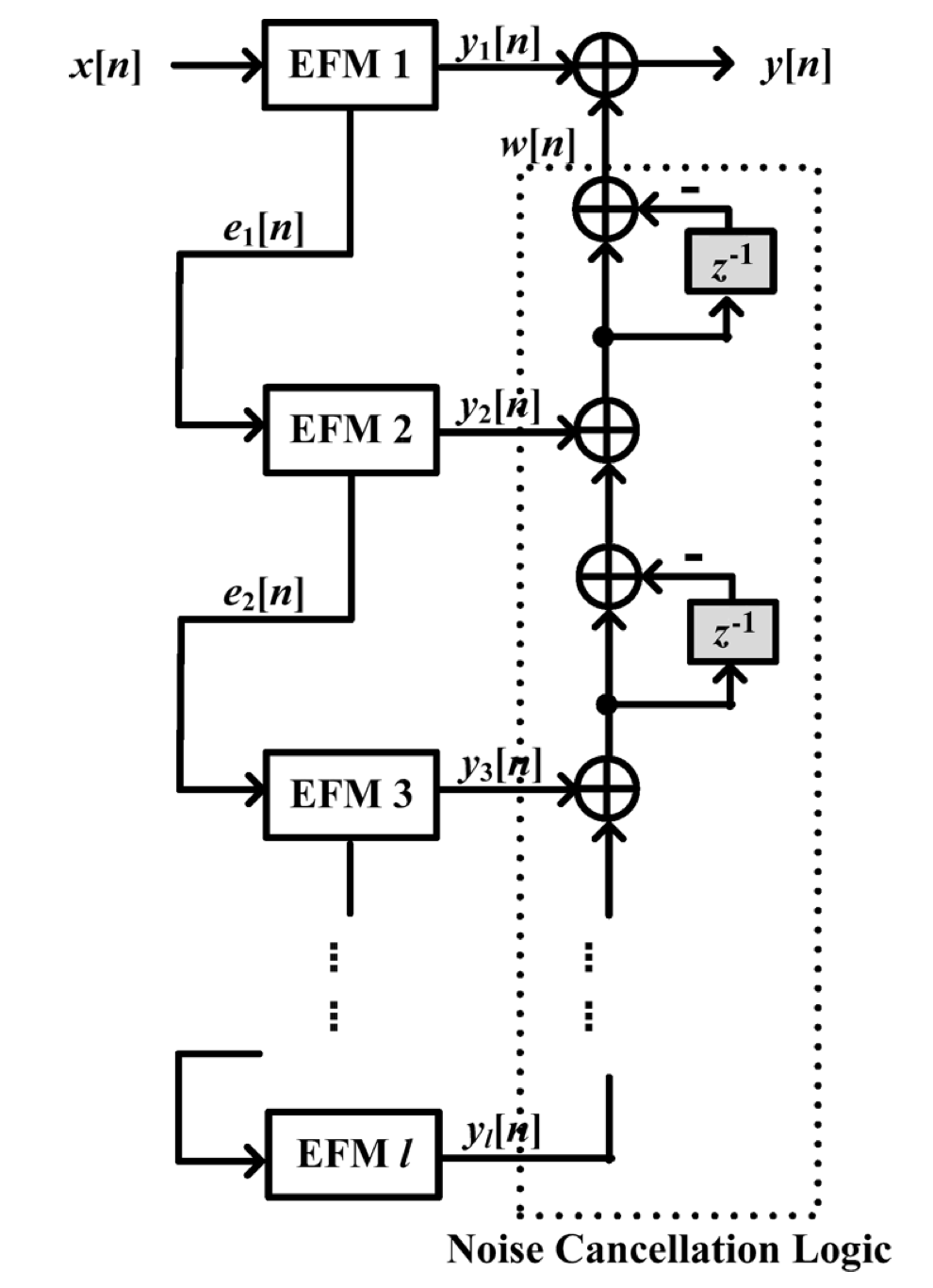
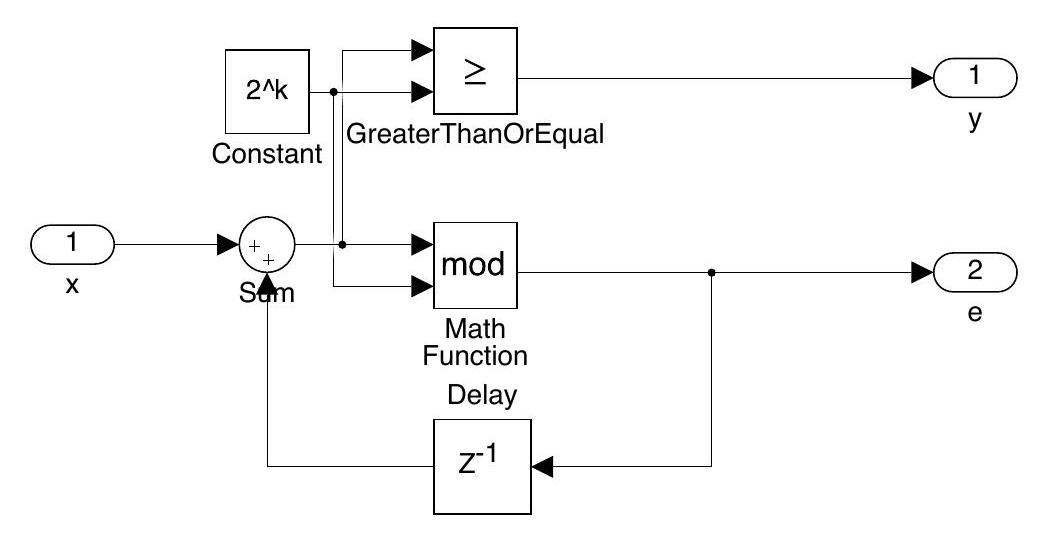
传统的 MASH 结构如上图所示，其一阶调制器 (first-order error feedback modulator, EFM) 如左边的图所示，其本质上是一个累加器，前一级的 EFM 误差作为后以及的输入。

HK-MASH 结构

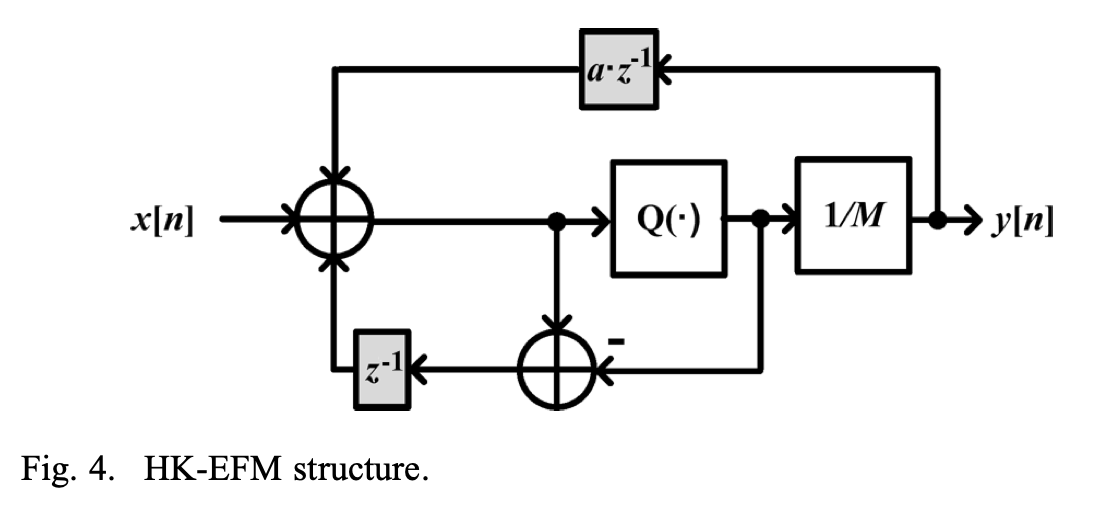
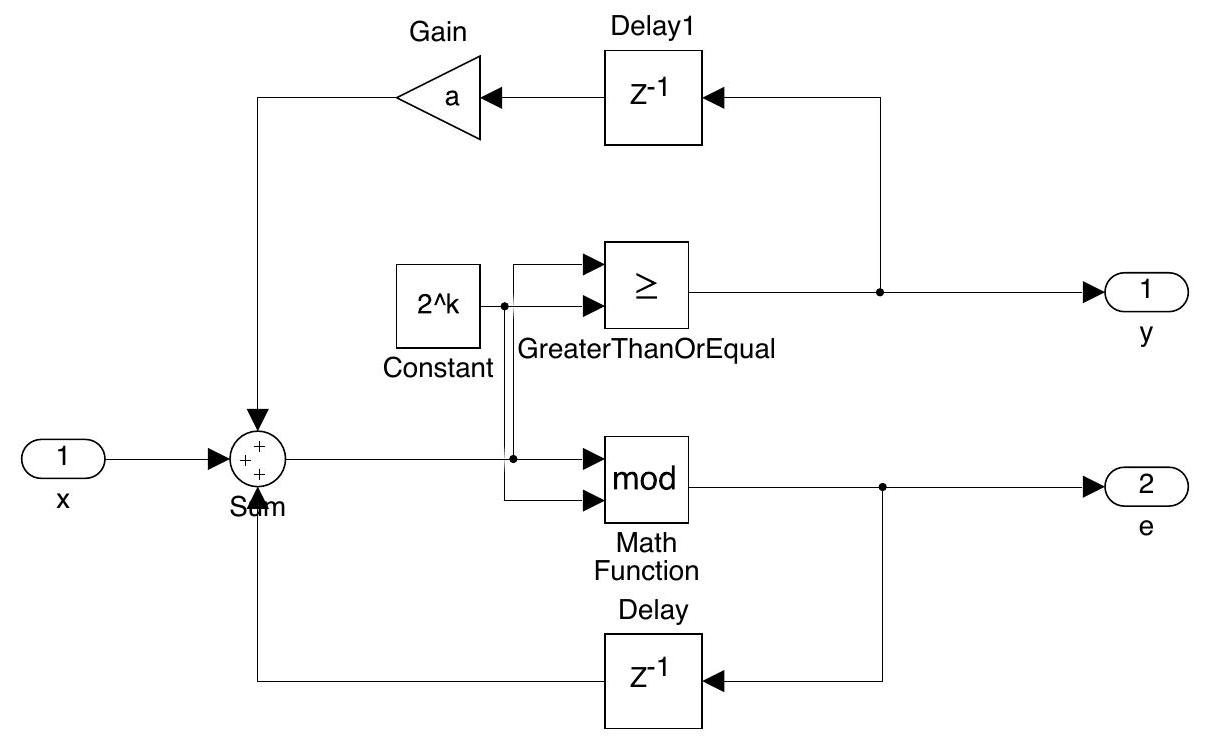
HK-MASH 结构的 EFM 如上图所示，其相比于原始的 EFM，加入了一个在输出 \(y[n]\) 到输入 \(x[n]\) 之间加入了一个增益为 \(a\) 的反馈通路，使得模 \((M-a)\) 成为一个质数，对于大多数输入其输出周期为 \((M-a)\)，因此对于 \(l\) 级的 MASH，其输出周期为 \((M-a)^l\)。

由于反馈的加入，HK-MASH 结构的输出平均值不再等于输入，而是呈线性关系： \[ Mean(Y) = Mean(X)/(M-a) \]

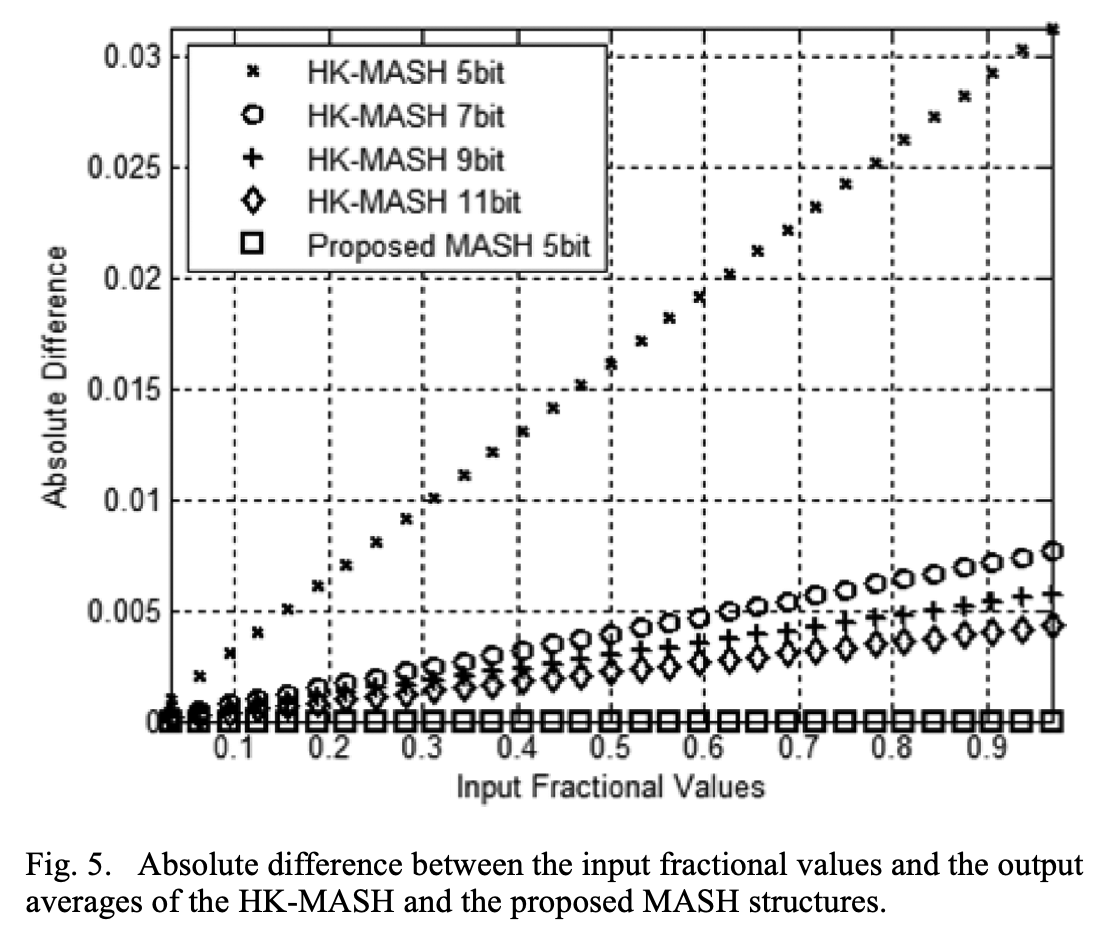
如果想让输出平均值为 \(\alpha\)，则输入值需要缩放为 \(\alpha(M-a)/M\)，因此 HK-MASH 结构的 DSM 不支持全范围输入，并且需要额外的电路来实现这个缩放过程。

SP-MASH

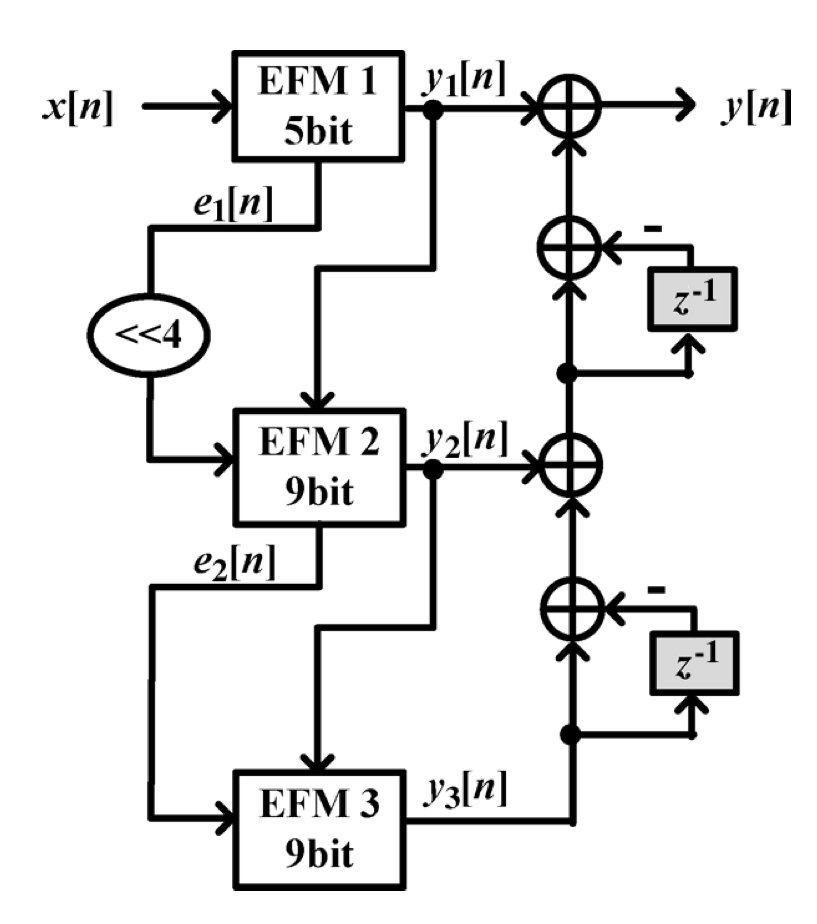
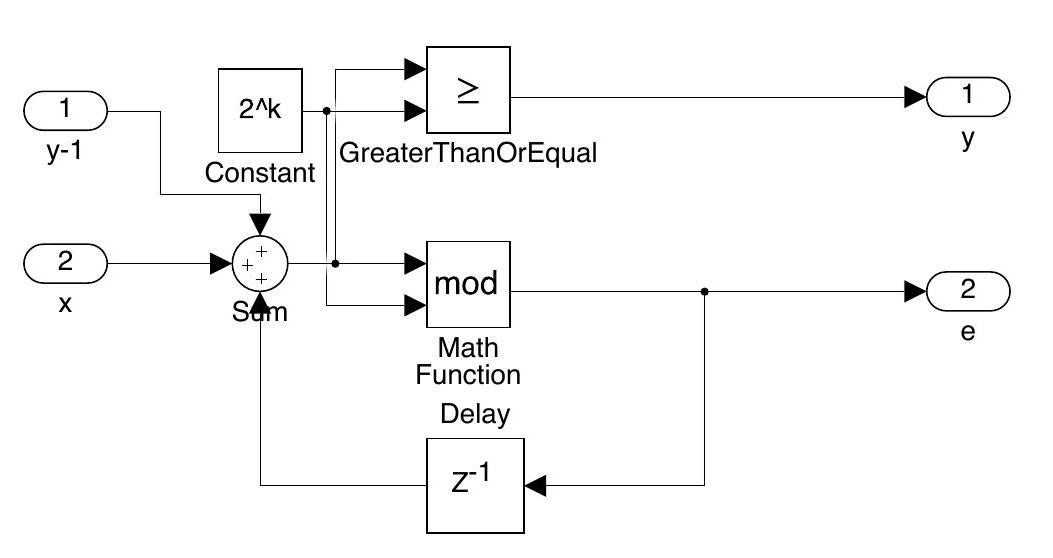
Spur-Free MASH 的结构如上图所示，相对于原始的 EFM，SP-EFM 增加了一个前一级的量化输出作为本级的输入。该结构的改动几乎不消耗额外的硬件资源，并且输入和输出是相等的，即输入时全范围的。

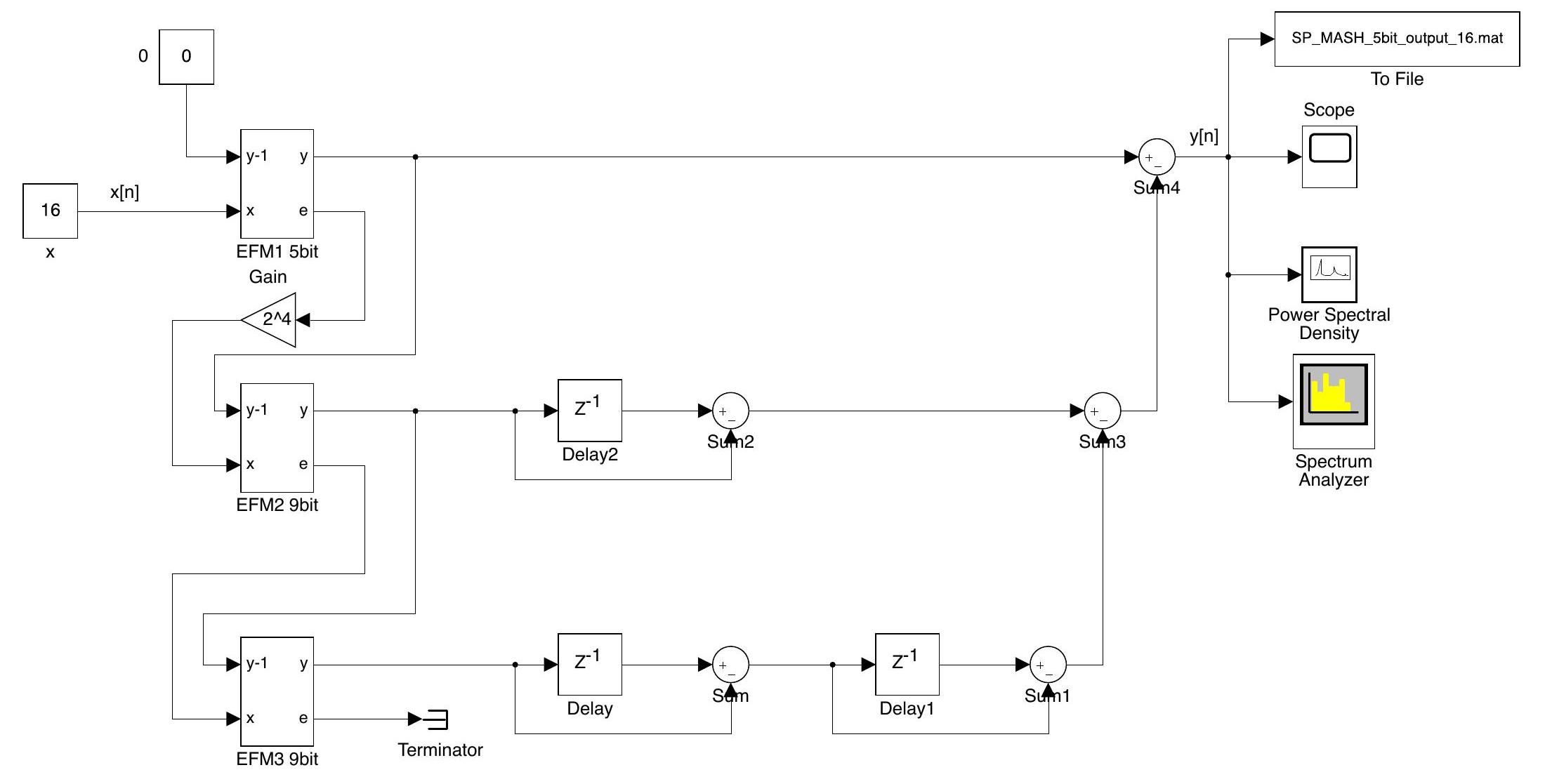
为了扩大输出的周期，可以增加除第一级之外的 EFM 的位数，例如上面的结构中，第一级设为 5bit，第二级和第三级设为 9bit，将第一级的量化误差左移 4 位再作为第二级的输入。

SP-MASH 的输出的周期为 \(N_1L^2\)，其中 \(L = 2^r\)，\(r\) 为后面几级的位宽；\(N_1\) 为第一级的输出周期，例如在上面的结构中 \(r=9\)，\(N_1\) 最小等于 2。

使用 Simulink 仿真

传统的 MASH 结构

HK-MASH

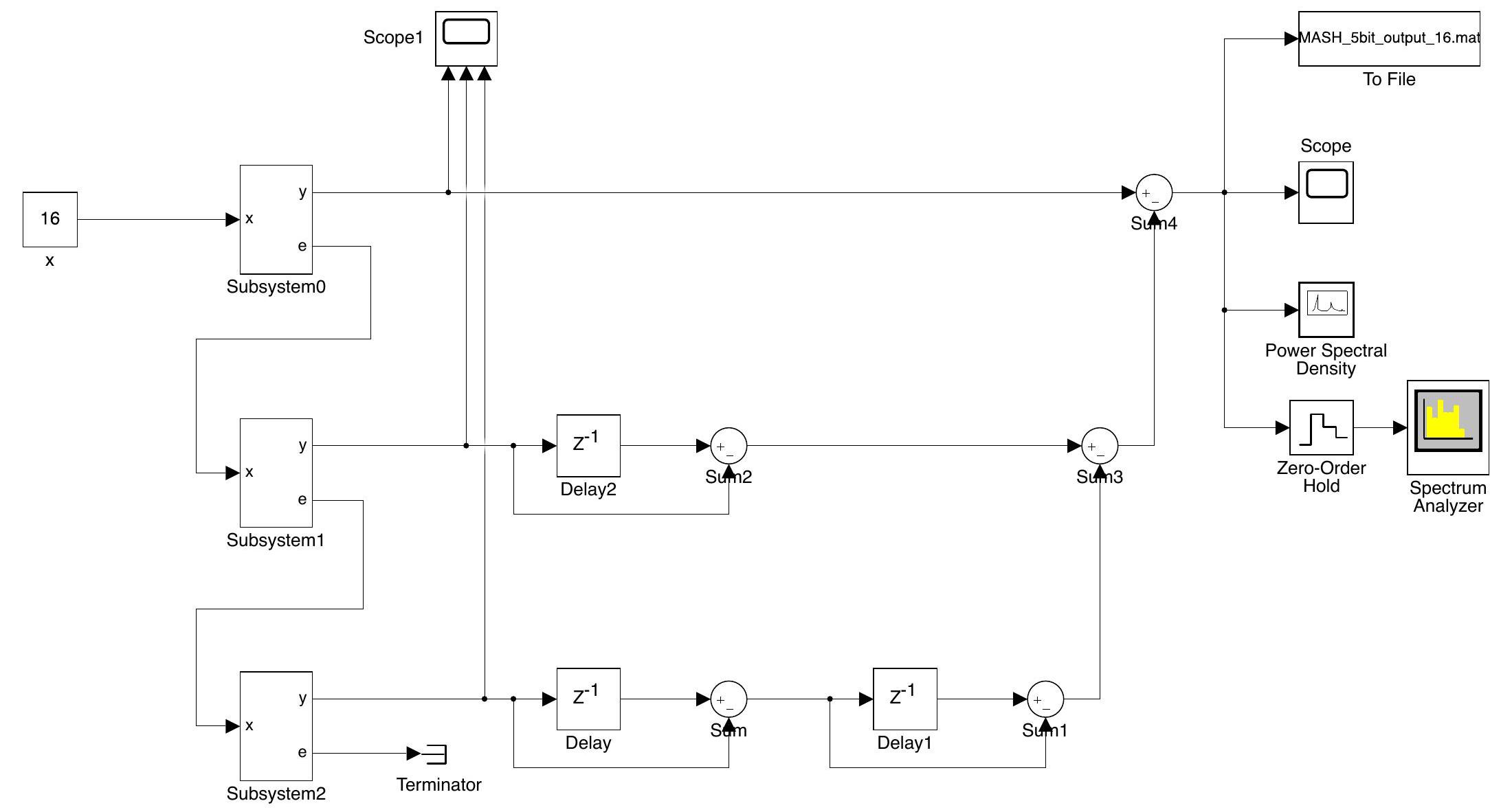
SP-MASH

仿真结果 MASH & HK-MASH & SP-MASH

输出序列

三种 MASH DSM 结构的输出序列如上图所示，由左到右分别是传统的 MASH、HK-MASH 和 SP-MASH，三种 MASH 均为 5bit，其中第一行为输入值 16（相当于 0.5），第二行输入值为 17（相当于 17/32）。

功率谱密度

三种 MASH DSM 结构的功率谱如上图所示，由左到右分别是传统的 MASH、HK-MASH 和 SP-MASH，三种 MASH 均为 5bit，其中第一行为输入值 16（相当于 0.5），第二行输入值为 17（相当于 17/32）。

结果分析&思考🤔

1. 从上面的时序的输出和功率谱密度都可以看出 HK-MASH 结构和 SP-MASH 结构对噪声的整形效果都比传统的 MASH 结构好；

2. 传统的 EFM 结构的输出序列的周期为： \[ N = \frac{M}{GCD(X, M)} \] 其中 \(GCD\) 表示最大公约数，\(X\) 为输入值，\(M\) 为 EFM 中计数器的最大值。

   因此在一些特定的输入时，其输出的周期很短，不能实现对噪声的整形，例如 5bit 的 EFM，\(M=2^5\)，当输入 \(X= 16\) 时，输出序列的周期为 2，三级 EFM​ 级联实现的 MASH1-1-1 结构的输出周期也只有 4，因此传统结构的 MASH DSM 周期偏短，在某些特定的输入下不能实现对噪声的整形。

3. HK-MASH 和 SP-MASH 结构都可以避免传统 MASH 周期短的问题，不过 HK-MASH 的输出不等于输入，需要消耗额外的硬件资源进行缩放，并且输入不是全范围；

4. 在低位宽下 HK-MASH 和 SP-MASH 结构相比于传统的 MASH 结构提升较为明显，例如上面的例子都是在 5bit 先进行比较的，个人觉得当位宽较大时，HK-MASH 和 SP-MASH 结构相比于传统的 MASH 结构优势就没有那么明显了，在 24bit 的 EFM 结构中验证了这个想法。

5. 就功率谱密度来看，感觉 SP-MASH 对比 HK-MASH 并没有明显的提升，我自己的仿真中没有论文中的差距那么大：

result in paper

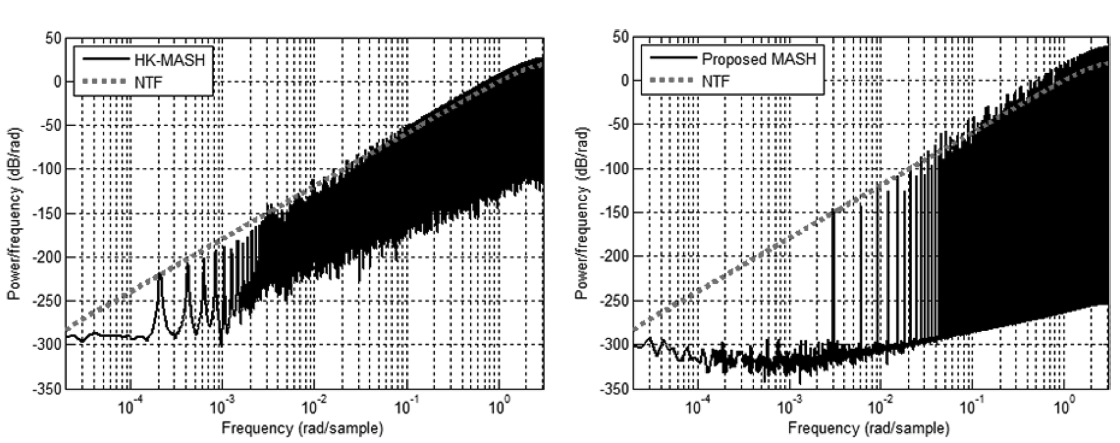
上面一行是我自己的仿真结果，下面一行是论文中的结果，输入都为 16。

参考文献

[1] Y. Liao, X. Fan and Z. Hua, "Influence of LFSR Dither on the Periods of a MASH Digital Delta–Sigma Modulator," in IEEE Transactions on Circuits and Systems II: Express Briefs, vol. 66, no. 1, pp. 66-70, Jan. 2019, doi: 10.1109/TCSII.2018.2828600.

[2] J. Song and I. Park, "Spur-Free MASH Delta-Sigma Modulation," in IEEE Transactions on Circuits and Systems I: Regular Papers, vol. 57, no. 9, pp. 2426-2437, Sept. 2010, doi: 10.1109/TCSI.2010.2043993.

PSD MATLAB 代码

%% PSD
% reference: https://zhuanlan.zhihu.com/p/50272016
clc
clear
ADD_WIN_FLAG = 1;
LOG_PLOT_FLAG = 1;
% name = "SP MASH 5bit input 17";
% figname = "results/sp_mash_5bit_17_psd.png";
% load("SP_MASH_5bit_output_17.mat");

name = "MASH 9bit input 255";
figname = "results/mash_9bit_255_psd.svg";
load("MASH_9bit_input_255.mat");

x = y.Data;
x = double(x);


% FFT 求功率谱密度
L = length(x);
% N = L;

% % 比当前长度大的下一个最小的 2 的次幂值
% N = 2^nextpow2(L);
% x_new = zeros(1, N-L);
% x = [x, x_new];

%%
% 取2的幂次方
N = 2^(nextpow2(L)-1);
x = x(1:N);

% 加窗
if ADD_WIN_FLAG
    wn=hann(N);  %汉宁窗
    x=x.*wn;   % 原始信号时域加窗
end

xdft = fft(x, N);
psdx = xdft.*conj(xdft)/N; % 双边功率谱密度，conj 共轭复数

% 加窗系数修正
if ADD_WIN_FLAG
    zz = wn.*wn;
    zz1 = sum(zz);
    psdx = psdx*N/zz1;
end

spsdx = psdx(1:floor(N/2)+1)*2; % 单边功率谱密度
spsdx(1) = psdx(1);

spsdx_log = 10*log10(spsdx); % 取log
spsdx_log(spsdx_log == -inf) = -300; % 处理 log10(0) 的情况

% 单边带
freq = 0:(2*pi)/N:pi;
% 双边带
% freq = 0:(2*pi)/N:(2*pi-(2*pi)/N);

% NTF 3阶
NTF = 3*20*log10(2*sin(freq/2));

if LOG_PLOT_FLAG
    semilogx(freq/pi, spsdx_log, freq/pi, NTF, '--')
else
    plot(freq/pi, spsdx_log, freq/pi, NTF, '--')
end
grid on
legend(name, 'NTF','Location', 'northwest')
title('Periodogram Using FFT')
xlabel('Normalized Frequency (\times\pi rad/sample)') 
ylabel('Power/Frequency (dB/rad/sample)')
saveas(gcf,figname)

%%
% periodogram 求功率谱密度
% win: hann rectwin
[h, w] = periodogram(x,rectwin(length(x)),length(x));
plot(w/pi, h)
% periodogram(x,rectwin(length(x)),length(x));
semilogx(w/pi, 10*log10(h))
grid on
legend(name, 'NTF','Location', 'northwest')
title('Periodogram Using FFT')
xlabel('Normalized Frequency (\times\pi rad/sample)') 
ylabel('Power/Frequency (dB/rad/sample)')
% test
% fs = 1000;
% t = 0:1/fs:5-1/fs;
% x = cos(2*pi*100*t) + randn(size(t));
% x = cos(2*pi*100*t);

%%
% pwelch
% fs = 100000;

% NTF
a = 1;
b = [1,-3,3,-1];
[h_ntf,w_ntf] = freqz(b,a,5000);

N = length(x);
win = hanning(N);  %汉宁窗
% win = rectwin(N);
nfft = N;
noverlap = 50;
[pxx,w] = pwelch(x, win, noverlap, nfft);

% plot(w/pi,10*log10(pxx))
semilogx(w/pi,10*log10(pxx),w_ntf/pi,20*log10(abs(h_ntf)), '--')
xlabel('\omega / \pi')
grid on
legend(name, 'NTF','Location', 'northwest')
title('Periodogram Using FFT')
xlabel('Normalized Frequency (\times\pi rad/sample)') 
ylabel('Power/Frequency (dB/rad/sample)')