0%

gmid 设计方法

发表于 更新于 分类于
本文字数： 4k 阅读时长 ≈ 4 分钟

gm/id 设计方法的优点

  • gm/Id对应Vov，通过其数值大小的选取来达到增益与带宽的折衷；
  • gm/Id方法是一种look-up table方法；
  • gm/Id方法为短沟道器件电路设计提供了比公式手算更准确的初值；
  • gm/Id方法为亚阈值设计提供了有力的工具。

长沟道模型回顾

在长沟道期间中，\(V_{ov}\) 表示过驱动电压： \[ V_{ov} = V_{gs} - V_{T} \]

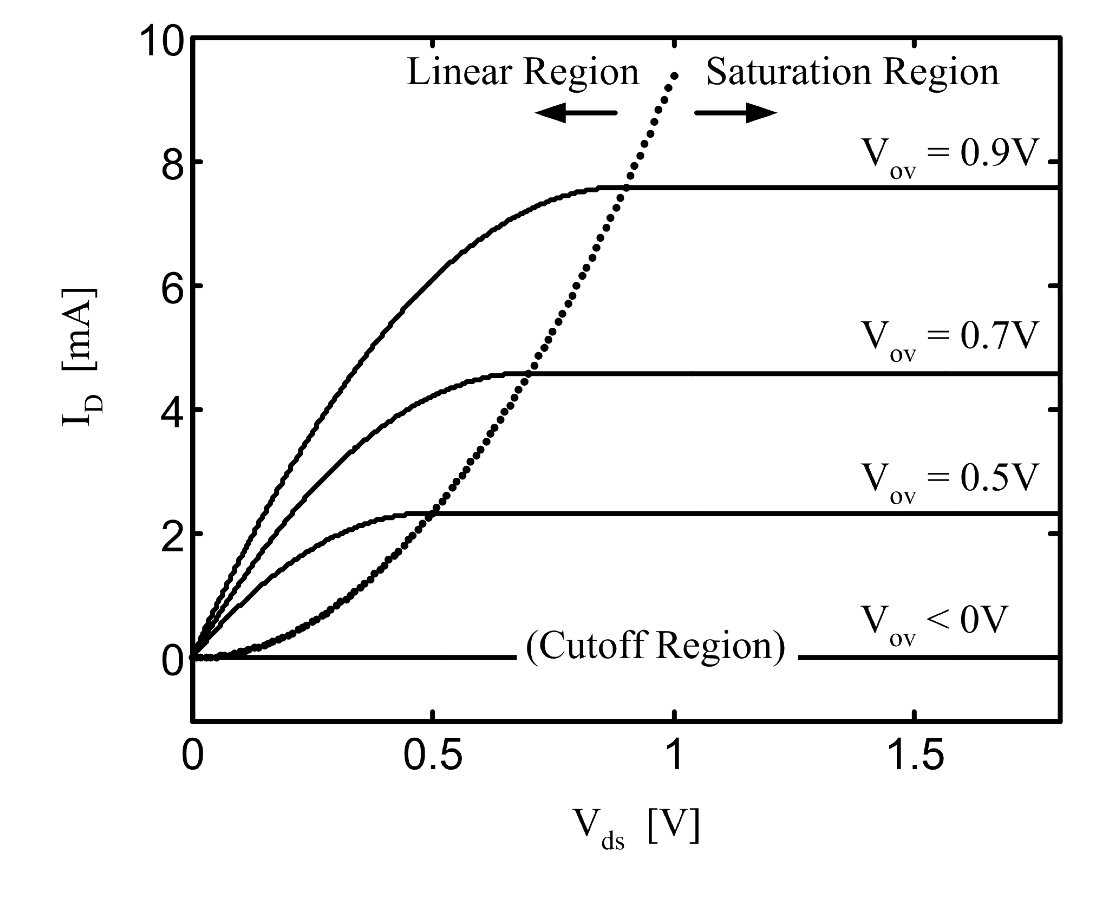
image-20210310201310417

在不同的 \(V_{ds}\) 和 \(V_{gs}\) 下，NMOS 管会工作在不同的区域：

  • 截止区：

    \(V_{ov}<0\) ( or \(V_{gs} < V_{T}\) )，

    \[ I_{D} = 0 \]

  • 线性区：

    \(V_{ov}>0\) and \(V_{ds} < V_{dsat}\)，

    \[ I_D = \frac{1}{2}\mu C_{ox}\frac{W}{L}[2V_{ov}V_{DS}-V_{DS}^2] \]

    \[ R_{on} = \frac{\partial V_{ds}}{\partial I_D} \]

  • 饱和区：

    \(V_{ov}>0\) and \(V_{ds} > V_{dsat}\)，

    \[ I_D = \frac{1}{2}\mu C_{ox}\frac{W}{L} V_{ov}^2 \]

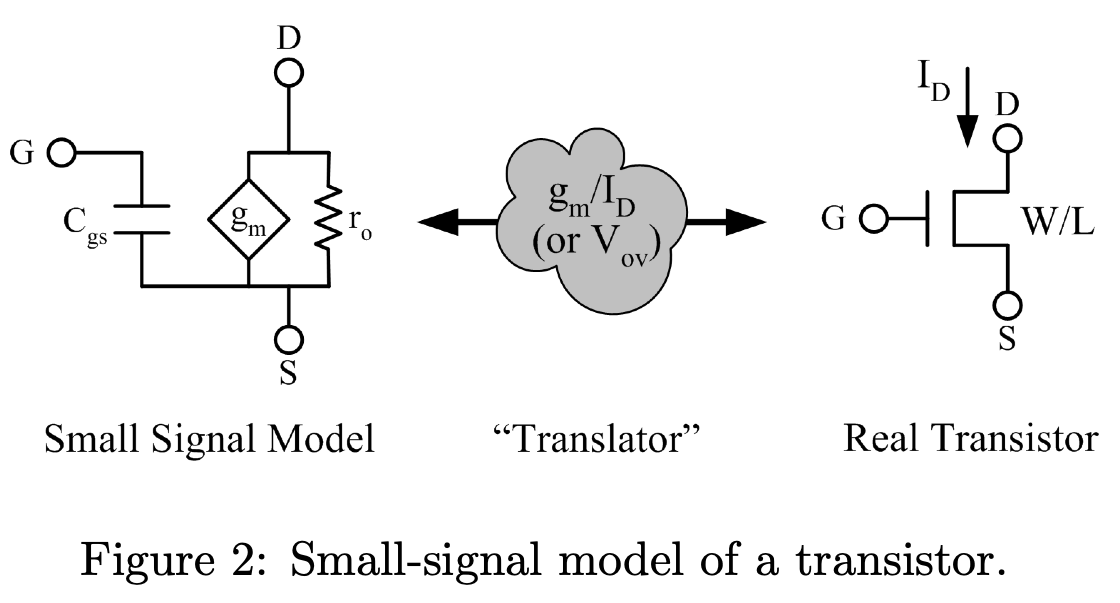
image-20210310202752762

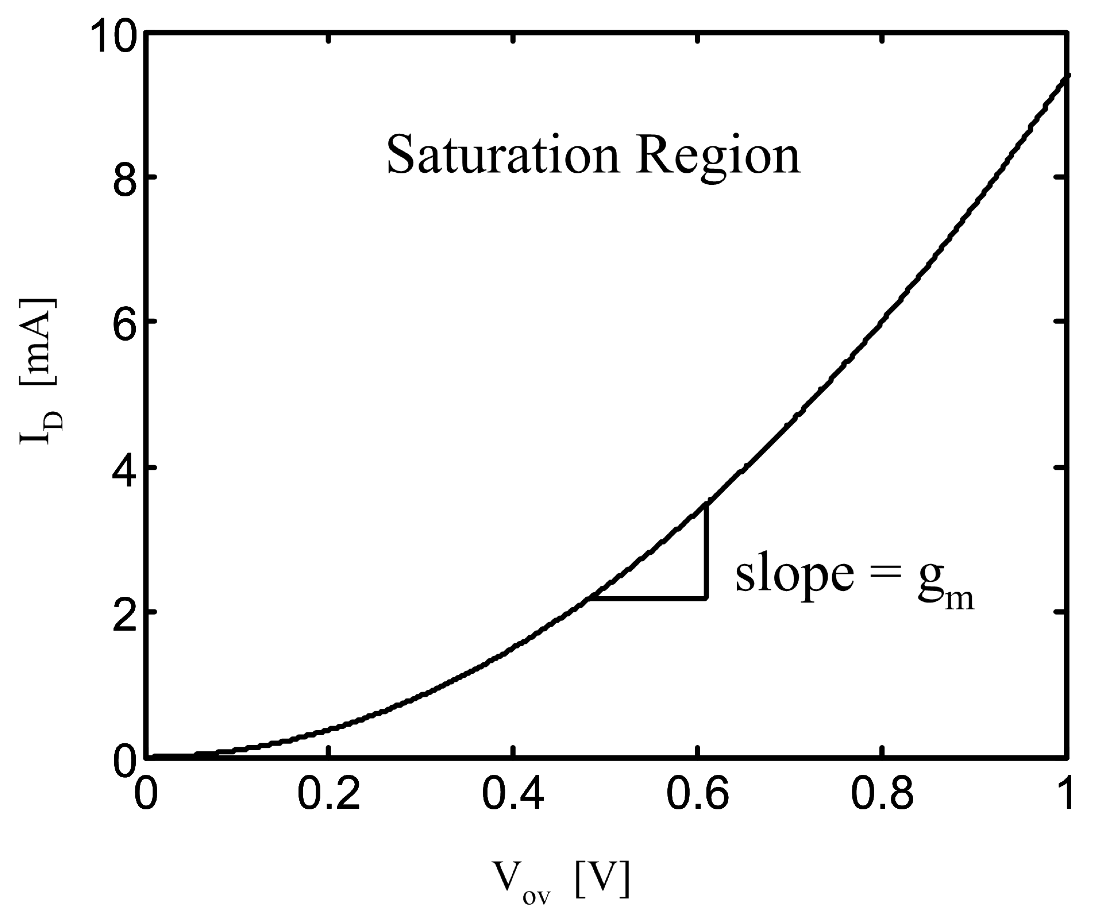
image-20210310202909324

在饱和区，\(I_D\) 是 \(V_{ov}\) 的函数，小信号模型中的 \(g_m\) 被定义为： \[ g_m = \frac{\partial I_D}{\partial V_{ov}} = \mu C_{ox}\frac{W}{L} V_{ov} \] 可以得到： \[ \frac{g_m}{I_D} = \frac{2}{V_{ov}} \] 上述公式表明了 \(g_m/I_D\) 和 \(V_{ov}\) 之间的关系。

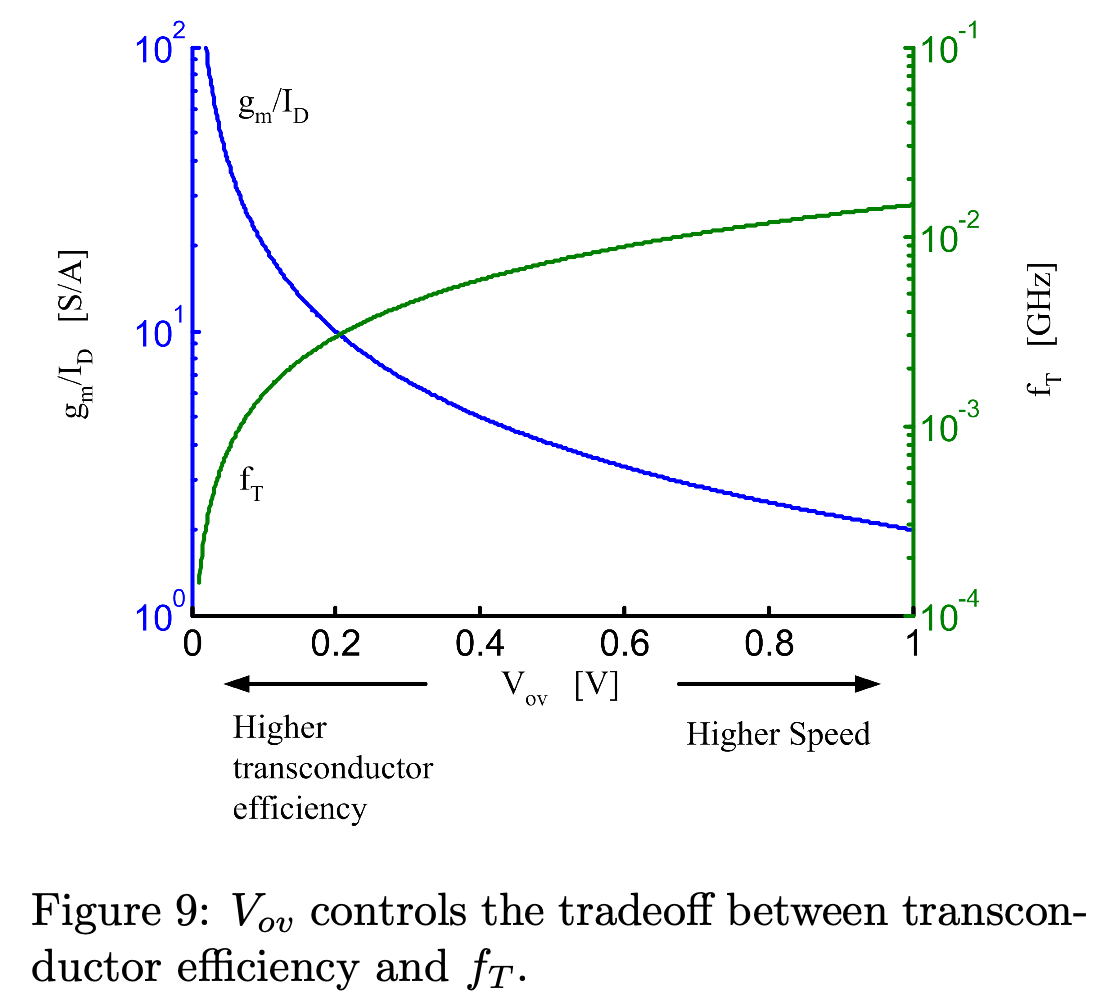
image-20210310213132752

定义晶体管的截止频率 (transit frequency) \(f_T\): \[ f_T = \frac{1}{2\pi}\frac{g_m}{C_{gs}} \] 其中 \(C_{gs} = \frac{2}{3}C_{ox}WL\)，则： \[ f_T = \frac{1}{2\pi}\frac{g_m}{C_{gs}} = \frac{1}{2\pi}\frac{2\mu V_{ov}}{3L^2} \] 从上面的等式中我们可以得到 \(g_m\) 和 \(f_T\) 之间的约束，Fig. 9 将其表示出来。

传统的 \(V_{ov}\) 设计方法

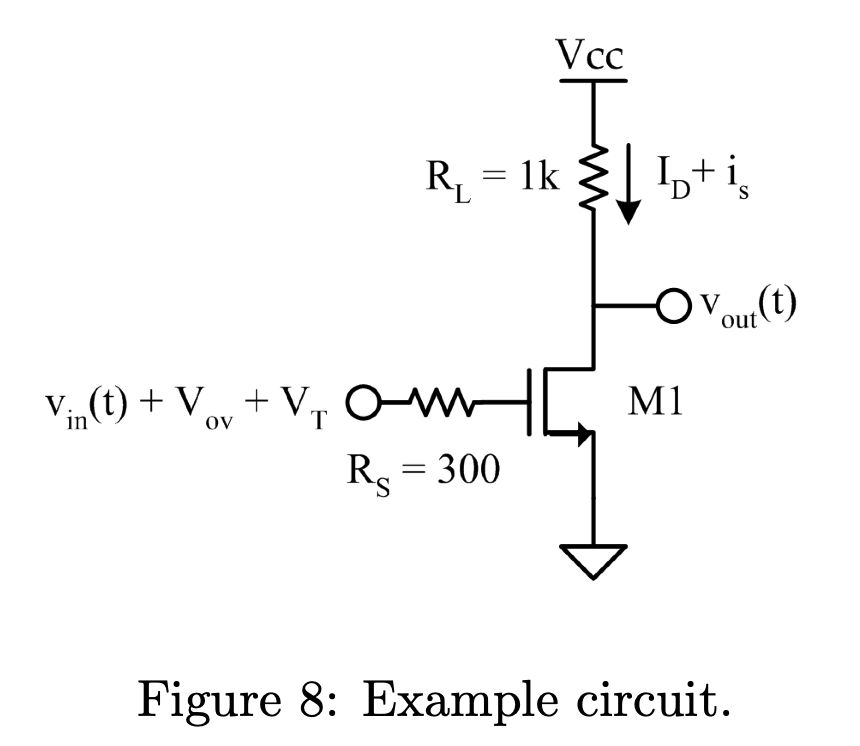
image-20210310203850046

在上图的电路中，假设 \(V_{ov} = 300 mV, I_D=1mA\)，则： \[ v_{out} = -i_s \cdot R_L=-v_{in} \cdot g_m \cdot 1k\Omega \]

\[ g_m = 2\frac{I_D}{V_{ov}} = \frac{2\cdot 1mA}{300 mV} = 6.7 \frac{mA}{V} \]

可以得到增益为： \[ \frac{v_{out}}{v_{in}}= -g_m \cdot R_L = -6.7\frac{mA}{V}\cdot 1k\Omega = -6.7 \frac{V}{V} \] 在上面的结构中假设要求带宽 \(500MHz\)，增益为 10，基于 \(V_{ov}\) 的设计流程如下：

  1. 为了保证增益，首先可以计算 \(g_m\)： \[ g_m = \frac{v_{out}}{v_{in}} / R_L = 10\frac{V}{V}/1k = 10mA/V \]

  2. 输入极点在 \(500MHz\)，可以以此计算 \(C_{gs}\)： \[ C_{gs} = \frac{1}{2\pi \times 300\Omega \times 500MHz} = 1.1pF \]

  3. 可以计算出截止频率： \[ f_T = \frac{g_m}{C_{gs}}=\frac{10mS}{1.1pF} = 9.4 GHz \]

  4. 通过 Fig. 9 可以知道： \[ V_{ov} \geq 75 mV \]

  5. 由此通过 Fig. 9 可以知道： \[ g_m/I_D \leq 26 mS/mA \]

  6. 最终可以得到： \[ I_D = \frac{g_m}{g_m/I_D} = \frac{10mS}{26mS/mA}=385\mu A \]

基于 \(V_{ov}\) 设计方法的缺点

image-20210310220510541

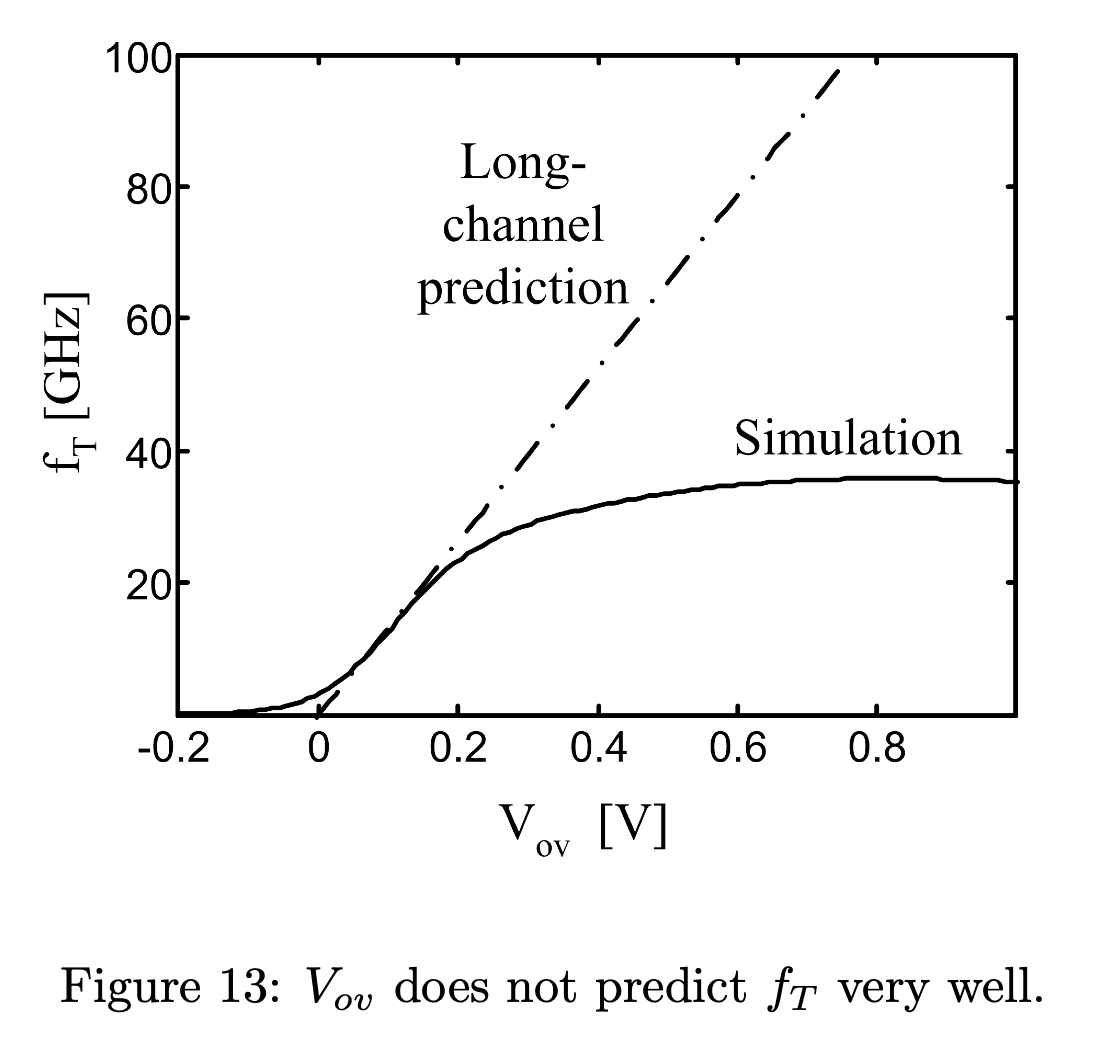
image-20210310220527243

从 Fig.12 可以看出，长沟道模型在 \(V_{ov}\) 较小 (弱反型区) 时 \(g_m/I_D\) 与 \(V_{ov}\) 的关系预测值与仿真值相差较大，在亚阈值区 (\(V_{ov} <0\)) 则完全失效。

从 Fig.12 可以看出，长沟道模型预测的 \(f_T\) 与 \(V_{ov}\) 的关系与仿真值相差较大。

基于 \(g_m/I_D\) 的设计方法

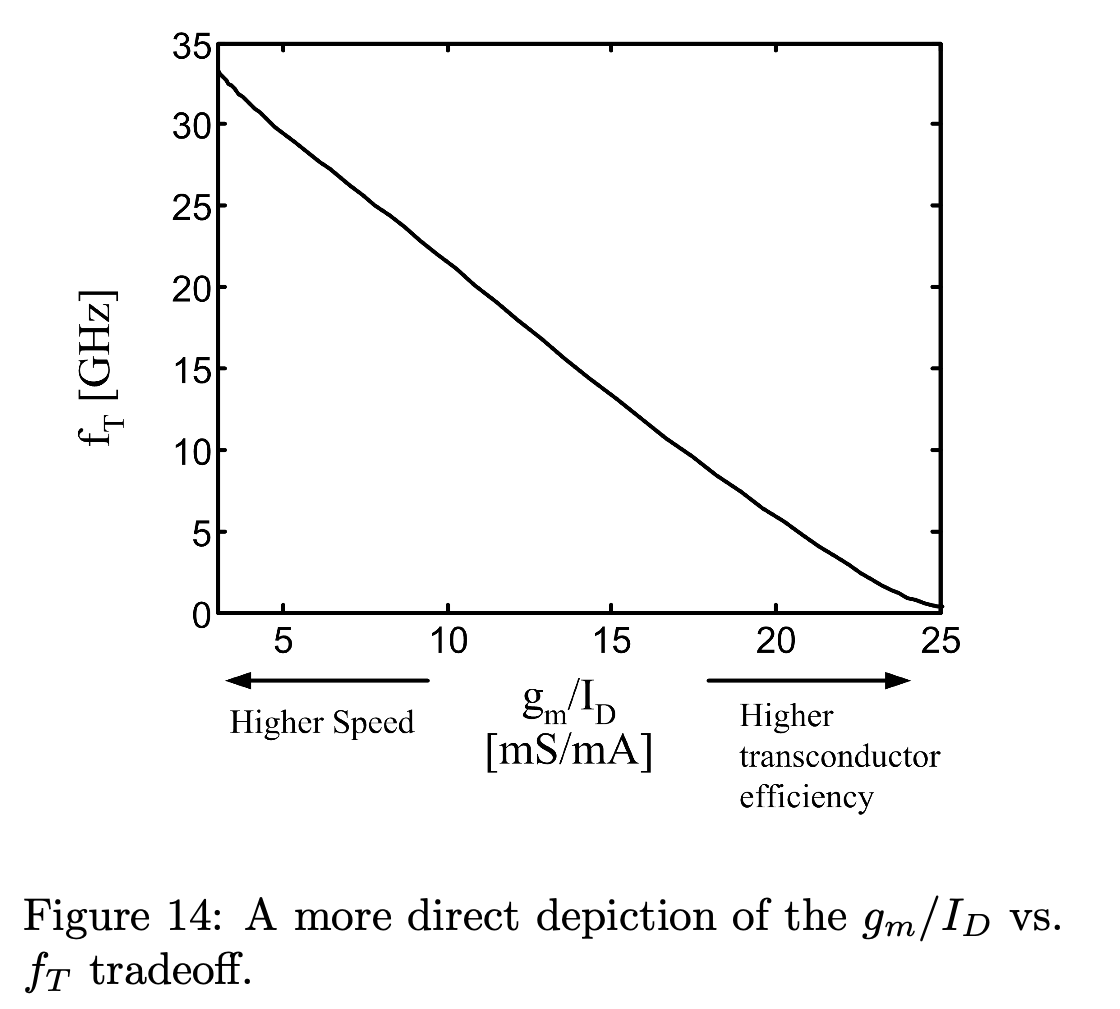
由于 \(g_m/I_D\) 与 \(V_{ov}\) 之间存在关系，则可以用 \(g_m/I_D\) 取代 \(V_{ov}\) 来表示与 \(f_T\) 的关系，原来 Fig.9 的关系可以用 Fig.14 来表示。

image-20210310221848963

设计流程

在 Fig.8 的结构中假设要求带宽 \(500MHz\)，增益为 10，基于 \(g_m/I_D\) 的设计流程如下：

  1. 为了保证增益，首先可以计算 \(g_m\)： \[ g_m = \frac{v_{out}}{v_{in}} / R_L = 10\frac{V}{V}/1k = 10mA/V \]

  2. 输入极点在 \(500MHz\)，可以以此计算 \(C_{gs}\)： \[ C_{gs} = \frac{1}{2\pi \times 300\Omega \times 500MHz} = 1.1pF \]

  3. 可以计算出截止频率： \[ f_T = \frac{g_m}{C_{gs}}=\frac{10mS}{1.1pF} = 9.4 GHz \]

  4. 通过 Fig.14 可以知道： \[ g_m/I_D \leq 17.5 mS/mA \]

  5. 最终： \[ I_D = \frac{g_m}{g_m/I_D} = \frac{10mS}{17.5mS/mA}=570\mu A \]

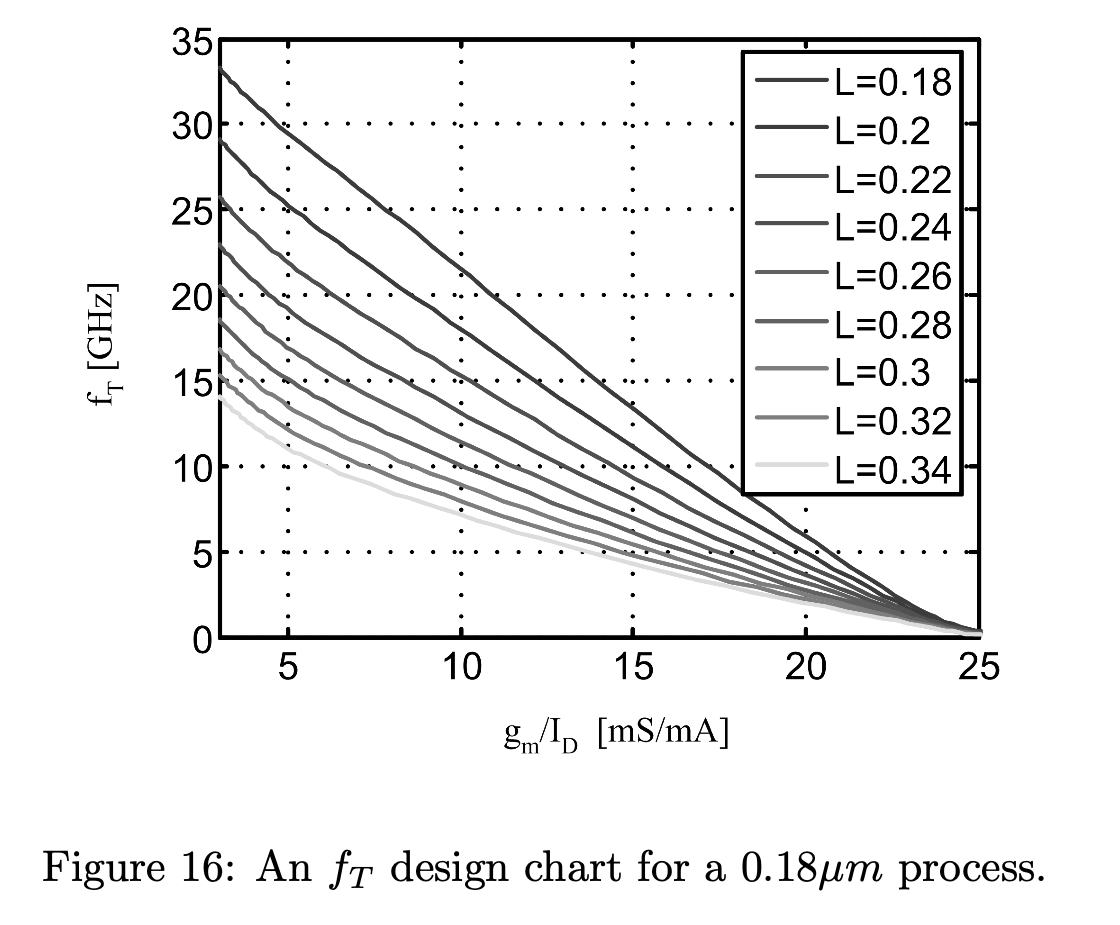
image-20210311101408375

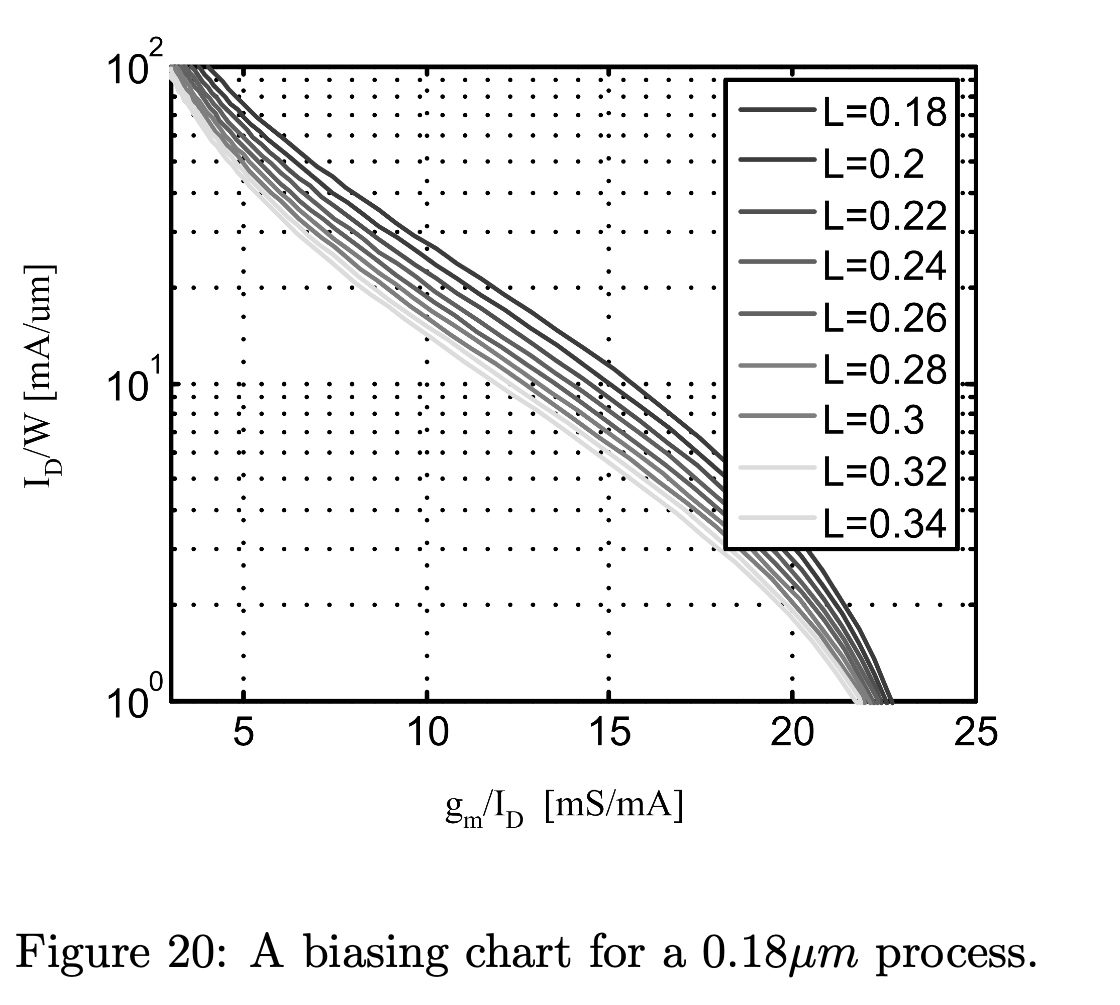
Fig.16 是不同的 \(L\) 下，\(f_T\) 与 \(g_m/I_D\) 的关系，越大的 \(L\) 通常意味着晶体管更慢。这就意味着要是没有其他的限制，我们就会选择最小的 \(L\)，这样晶体管速度最快，面积也最小。因此还需要一个限制会影响 \(L\) 的选取，这个限制就是 \(r_0\)。

考虑 \(r_0\)

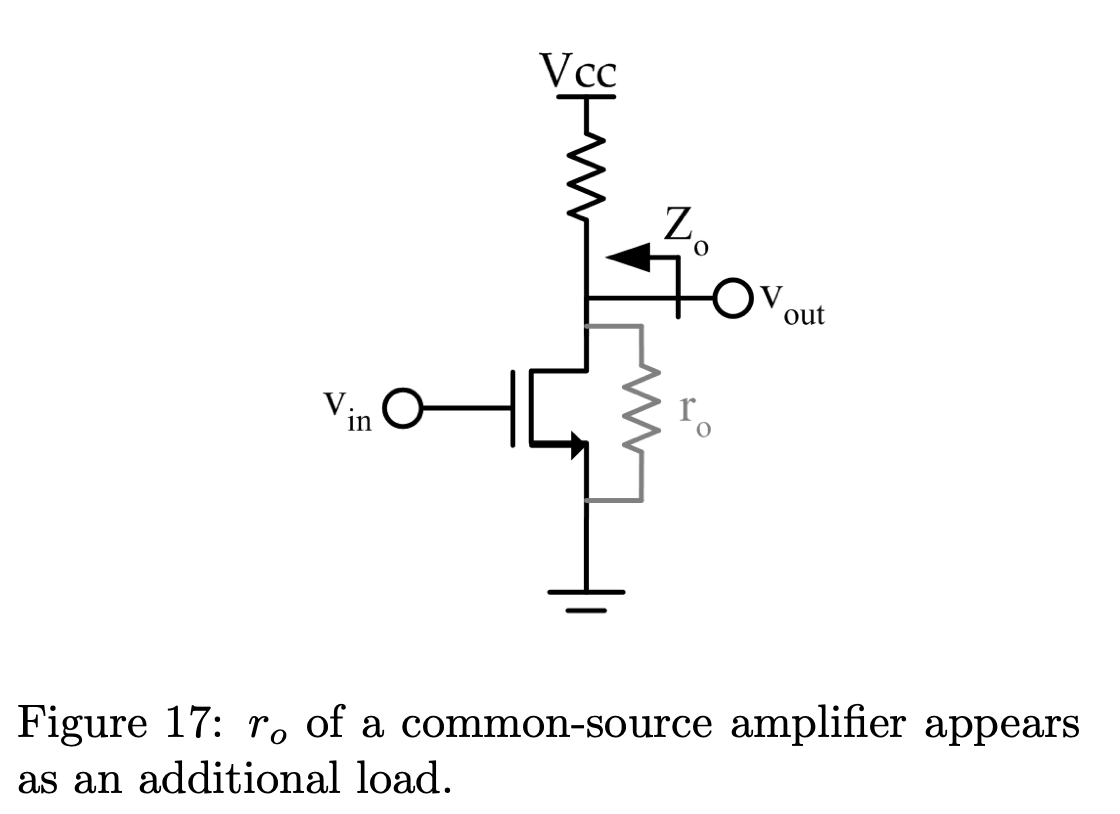
image-20210311095357398

从上图可以看到 \(r_0\) 相当于一个和 \(R_L\) 并联的负载，但我们考虑 $R_L $ 时，可以忽略 \(R_L\) 只考虑 \(r_0\)。则： \[ Intrinsic \ \ Gain = g_mr_0 (\frac{V}{V}) \] \(Intrinsic \ \ Gain\) 是晶体管可以达到的最大增益。

image-20210311100239741

从 Fig.19 中可以看到不同的 \(L\) 对应不同的 \(g_mr_0(Intrinsic \ \ Gain)\)。

由于 \(r_0\) 与 \(V_{ds}\) 有关，这里的假设是 \(V_{ds} = V_{DD}/2\)。

考虑 \(W\)

通过 Fig.16 和 Fig.19 可以确定 \(L\) 和 \(g_m/I_D\)：为了满足增益的要求，通过 Fig.19 确定了 \(L\)；为了满足 \(f_T\) 的要求，通过 Fig.16 确定了 \(g_m/I_D\)；通过 \(g_m/I_D\) 和 \(g_m\) 确定了 \(I_D\)。最后剩下的没有确定的量就是 \(W\)。

image-20210311102457544

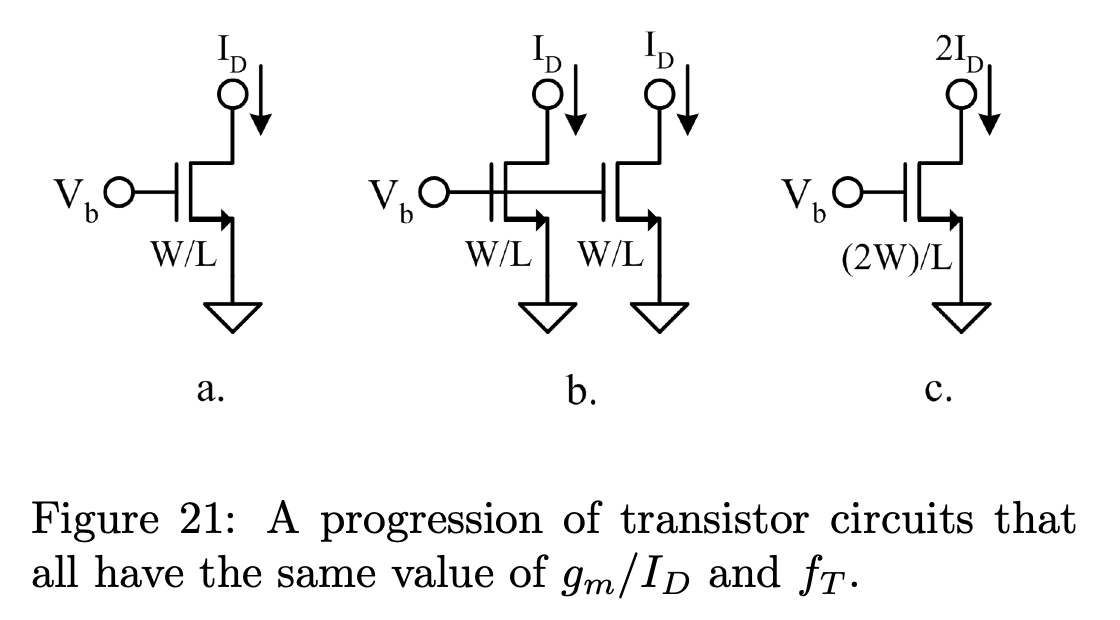
image-20210311104821336

在 Fig.21 中，由于 \(V_b\) 和 \(V_{DS}\) 相等，因此 a 和 b 的 \(g_m\) 、\(C_{gs}\) 相同，而 b 由于并联了两个晶体管，由此 \(I_D\) 是 a 的两倍，c 和 b 等价。由此只要保证 \(g_m\)-to-\(I_D\) 和 \(g_m\)-to-\(C_{gs}\) 的比率相等，W 变为原来的 N 倍，\(I_D\) 也变为原来的 N 倍，而 \(g_m/I_D\) 和 \(f_T\) 不变。

A Top-to-Bottom Design Example

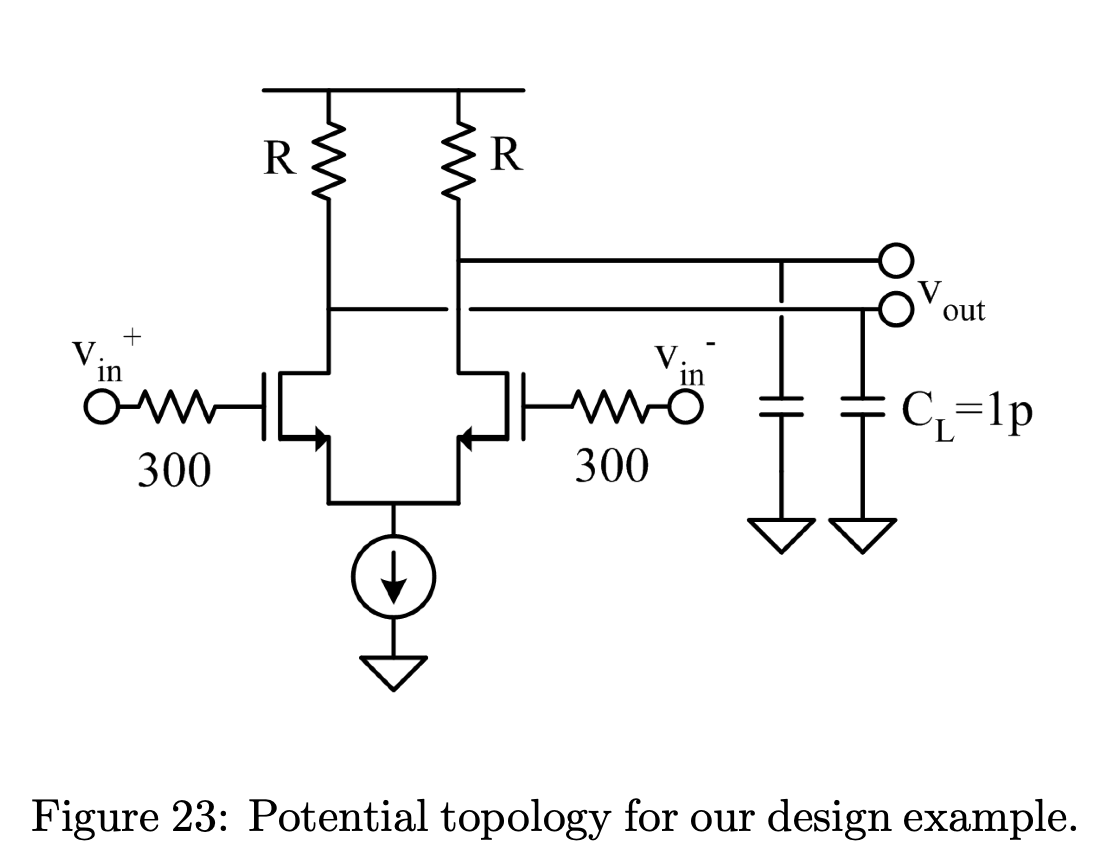
image-20210311095035057

设计一个差分放大器，结构如 Fig.23 所示，要求：

  • Gain of ≈ 10
  • Bandwidth of ≈ 200MHz
  • Drive a 1pF load
  • Be driven by a 300Ω
  • Lowest possible power

搭建电路

OPA

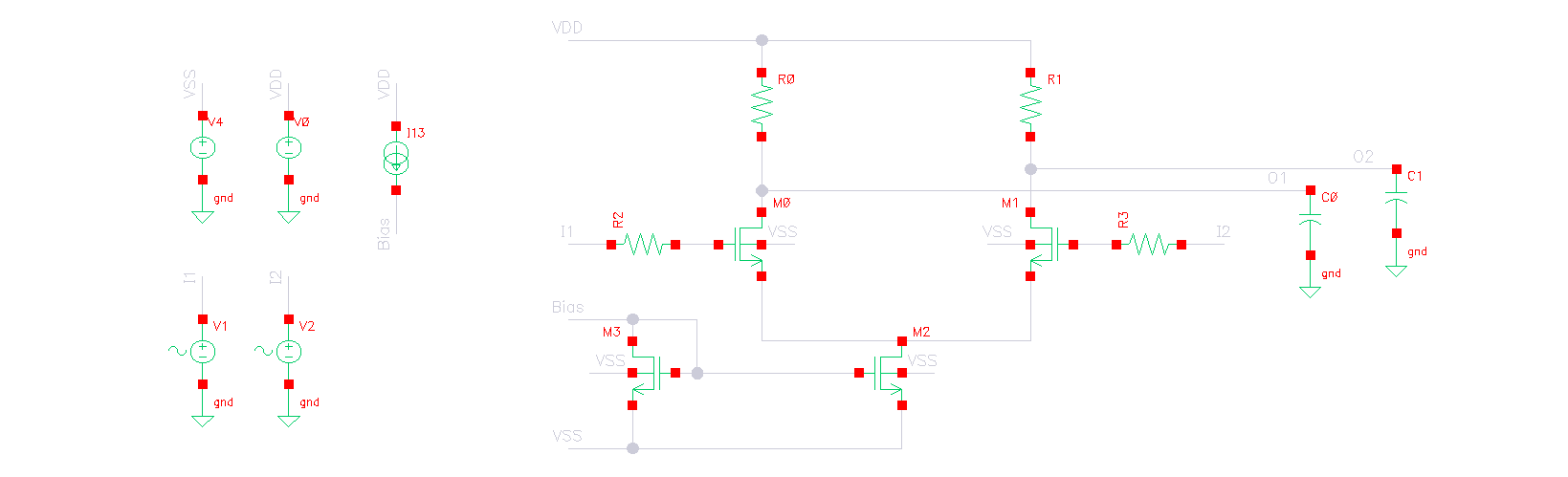
获取晶体管参数

通过 cadence 仿真并用 MATLAB 处理数据并画出图形。




Figure 25: Fruquency and Gain Tradeoff



Figure 26



Figure 27



Figure 28

选择参数

  1. 首先确定 \(L\)，通过 Fig.25，选取 \(L=340n m\)，在 \(g_m\) 选取中等值 (15) 时，Intrinsic Gain 大约是 100，这意味着它只会对整体增益产生10％的影响。 \[ L = 340n \]

  2. 下一步是计算 R 的值： \[ R = \frac{1}{2\pi \times C_L \times 200MHz} = 800 \Omega \]

  3. 因此通过增益可以确定 \(g_m\)： \[ g_m = \frac{Gain}{R}= 12.5mS \]

  4. 由于 200MHz 并不是唯一的一个极点，300Ω 的输入电阻与 \(C_{gs}\) 会产生第二个极点，为了减少第二个极点对系统的影响，将第二个极点设置在第一个极点的10倍处： \[ C_{gs} = \frac{1}{2\pi \times 300\Omega \times 2GHz} = 265 fF \]

  5. 有了 \(g_m\) 和 \(C_{gs}\)，可以计算出截止频率： \[ f_{T} = \frac{1}{2\pi}\frac{g_m}{C_{gs}} = \frac{1}{2\pi}\frac{12.5mS}{265fF}=7.5GHz \]

  6. 有了 \(L\) 和 \(f_T\)，通过 Fig.25 可以得到 \(g_m/I_D\)： \[ g_m/I_D = 15mS/mA \]

  7. 有了 \(g_m/I_D\) 和 \(g_m\)，可以计算出 \(I_D\)： \[ I_D = \frac{g_m}{g_m/I_D}= \frac{12.5}{15}\approx 0.83mA \]

  8. 最后，通过 Fig.27 找出对应的 \(I_D/(W/L)\) 为 \(2.2046e-06\)，因此可以计算出 \(W/L = 376\)： \[ W = 128um \]

仿真结果

db

仿真的结果显示增益为 18.7 dB，带宽为 164.4 MHz。

Reference

[1] Stanford ee214b的课件

-------The end of this article  Thank you for your reading-------