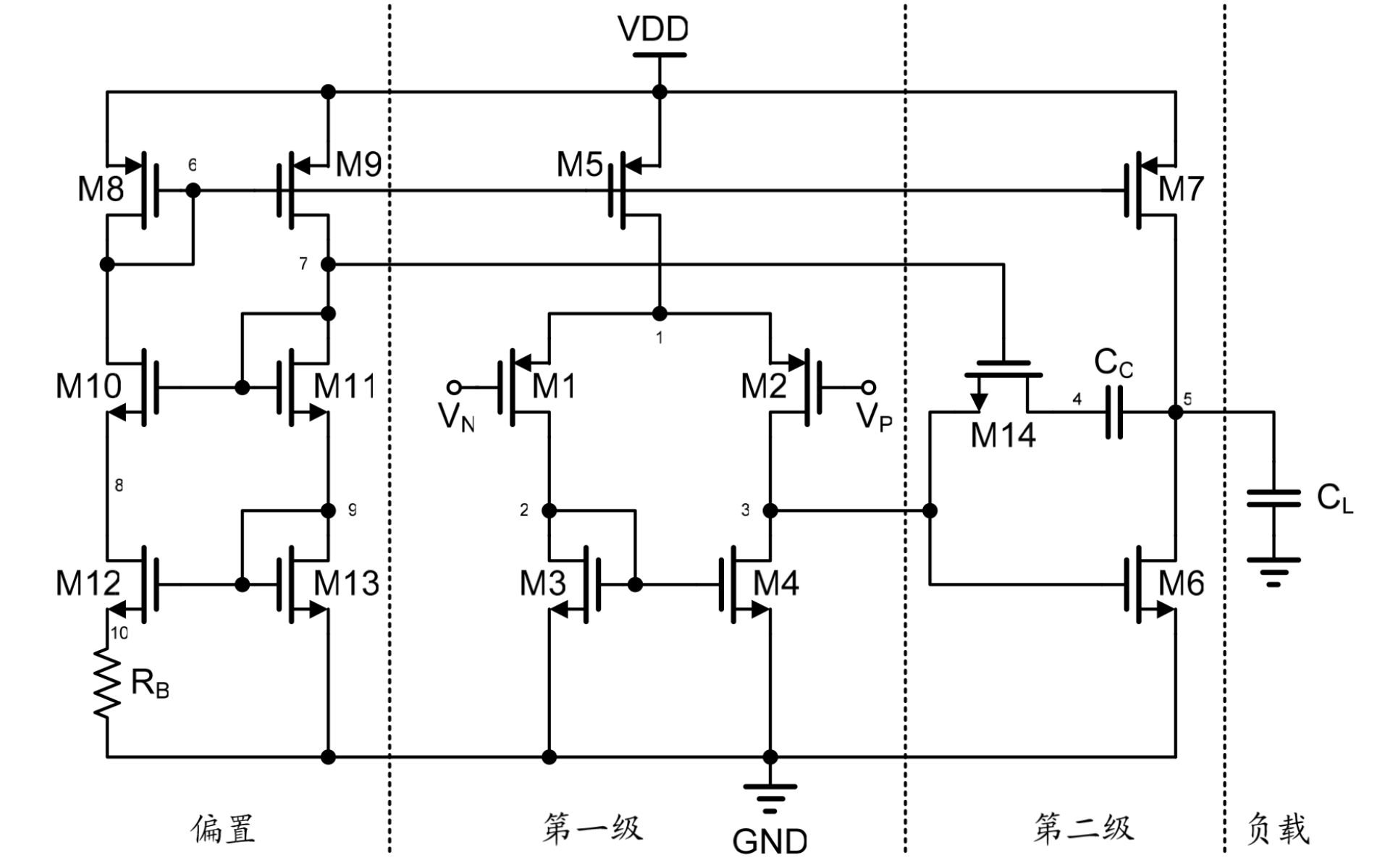
最基本的 CMOS 二级密勒补偿运算跨导放大器结构如图所示,主要包括四个部分:第一级输入级放大电路、第二级放大电路、偏置电路和相位补偿电路。
电路分析
输入级电路由 M1~M5 组成;
输出级电路由 M6、M7 组成,M6 为共源放大器,M7 为其提供恒定的偏置电流,同时作为第二级输出负载。相位补偿电路由 M14 和 Cc 构成,M14 工作在线性区,可等效为一个电阻,与电容 Cc 一起跨接在第一级和第二级输出之间,构成 RC 密勒补偿。
静态特性
不考虑 M14,电路的等效模型如下图所示:
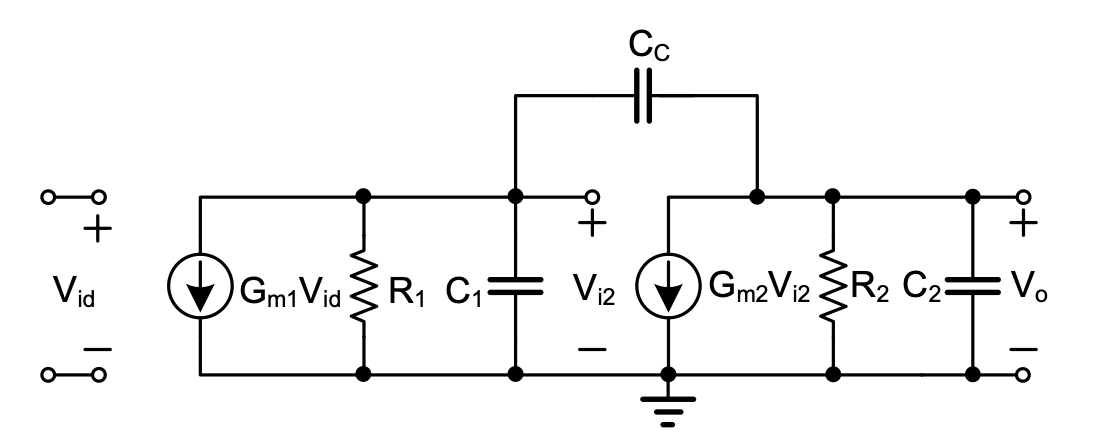
第一级和第二级都是跨导放大器,M1 和 M2 相同,则第一级的跨导为: \[ G_{m1} = g_{m1}=g_{m2} \]
第一级的输出电阻为: \[ R_1 = r_{o2} || r_{o4} \] 则第一级的增益为: \[ A_1 = G_{m1}R_1 = g_{m2}(r_{o2} || r_{o4}) \] 对于第二级,M6、M7 为共源放大器,则: \[ G_{m2} = g_{m6}=\frac{2I_{DS6}}{V_{GST6}} \]
\[ R_2 = r_{o6}||r_{o7} \]
其中 \(V_{GST6} = V_{GS6} - V_{TH6}\)。
则第二级的电压增益为: \[ A_2 = -G_{m2}R_2 = -g_{m6}(r_{o6}||r_{o7}) \] 故总的直流开环电压增益为: \[ A_0 = A_1A_2=-g_{m2}g_{m6}(r_{o2} || r_{o4})(r_{o6}||r_{o7}) \] 为了得到较高的增益,应当选取较小的过驱动电压和较大的沟道长度。
频率特性
在等效电路图中,第一级的输出节点的电容 \(C_1\) 为: \[ C_1 = C_{GD2} + C_{DB2} + C_{GD4} + C_{DB4} + C_{GS6} \] 第二级的输出节点的电容 \(C_2\) 为: \[ C_2 = C_{DB6} + C_{DB7} + C_{GD7} + C_{L} \] 一般,\(C_L\) 远大于晶体管电容,所以 \(C_2\) 远大于 \(C_1\),对节点 3 和节点 5 运用 KCL,得: \[ G_{m1}V_{id}+\frac{V_{i2}}{R_1}+sC_1V_{i2}+sC_c(V_{i2}-V_o) = 0 \]
\[ G_{m2}V_{i2}+\frac{V_{o}}{R_2}+sC_2V_{o}+sC_c(V_{o}-V_{12}) = 0 \]
联立上面两式,消去中间量 \(V_{i2}\) 得到电路的传输函数: \[ \frac{V_o}{V_{id}} = \frac{G_{m1}(G_{m2}-sC_c)R_1R_2}{as^2+bs+1} \] 其中 \(a=[C_1C_2+C_c(C_1+C_2)]R_1R_2 \\ b=C_1R_1+C_2R_2+C_c(G_{m2}R_1R_2+R_1+R_2)\)
由传输函数的分子可以得到一个位于右半平面的零点: \[ f_z = \frac{G_{m2}}{2\pi C_c}=\frac{g_{m6}}{2\pi C_c} \] 分析传输函数的分母,对于 \(as^2+bs+c=0\) 的方程,如果有两个相距很远的实根,则 \(s_1\approx -c/b, s_2\approx -b/a\)。由此得到: \[ s_1 = -\frac{1}{C_1R_1+C_2R_2+C_c(G_{m2}R_1R_2+R_1+R_2)} \]
\[ s_2 = -\frac{C_1R_1+C_2R_2+C_c(G_{m2}R_1R_2+R_1+R_2)}{[C_1C_2+C_c(C_1+C_2)]R_1R_2} \]
从而得电路主极点为: \[ f_d = \frac{s_1}{2\pi}=\frac{1}{2\pi R_1 [C_1+C_c(1+G_{m2}R_2)]} \] 通常 \(C_1\) 远小于 \(C_c\),且 \(G_{m2}R_2\) 远大于 1,上式可以近似为: \[ f_d = \frac{1}{2\pi R_1R_2G_{m2}C_c} \] 而次极点为: \[ f_{nd} =\frac{s_2}{2\pi}=\frac{G_{m2}C_c}{2\pi (C_1C_2 + C_1C_c+C_2C_c)} \] 单位增益带宽: \[ GBW = A_0f_d= G_{m1}G_{m2}R_1R_2 \times \frac{1}{2\pi R_1R_2G_{m2}C_c} = \frac{g_{m2}}{2\pi C_c} \] 由 \(g_m = \mu C_{ox} (W/L) (V_{GS}-VT)\) 得: \[ GBW = \frac{1}{2\pi C_c}\mu_p C_{ox}(\frac{W}{L})_2V_{GST2} \] 得到高的 GBW 就需要增大 M1 和 M2 管的过驱动电压或者减小其沟道长度,这与提高增益的要求是相互抵触的,而且管子面积的减小也会使得噪声性能变差,所以在设计电路的时候,需要根据具体应用和设计指标进行权衡。
GBW 也可以写成电流有关的形式 ( \(g_m = \mu C_{ox} (W/L) (V_{GS}-VT) = 2I_D/V_{GST}\) ): \[ GBW = \frac{I_{DS2}}{\pi C_c V_{GST1}} \] 上式说明,在选定了补偿电容和过驱动电压时,电路的单位增益带宽与功耗成正比。而电路设计时一般会对功耗有限制,由此为了得到高的 GBW,需要合理分配各支路的电流。
第二极点可以近似为: \[ f_{nd} = \frac{g_{m6}}{2\pi C_L} \] 一般而言,出于电路稳定的需要,为了达到 45° 的相位裕量,第二极点必须在 1.22GBW 之外,而若要有 60° 相位裕量的话,第二极点必须高于 2.2GWB。
相位补偿
\[ \frac{1}{R_zC_c}\approx1.2\frac{g_{m1}}{C_c} \]
即: \[ g_{m1}R_z\approx\frac{1}{1.2} \] 若令 \(V_{GST1}=V_{GST14}\),则: \[ \frac{(W/L)_{14}}{(W/L)_{1}} \approx1.2\frac{\mu _p}{\mu _n} \]
偏置电路
偏置电路由 M8~M13 构成。
镜像电流源 M8 和 M9 使得 M13 和 M12 的电流相等,都为 \(I_B\),则: \[ I_B = \frac{1}{2}\mu C_{ox}(\frac{W}{L})_{12}(V_{GS12}-V_T)^2 = \frac{1}{2}\mu C_{ox}(\frac{W}{L})_{13}(V_{GS13}-V_T)^2 \] 而: \[ V_{GS13} = V_{GS12}+I_BR_B \] 由上面两式可以得到: \[ I_B = \frac{2}{\mu C_{ox}(W/L)_{12}R_B^2}(\sqrt{\frac{(W/L)_{12}}{(W/L)_{13}}}-1)^2 \] 可以看到 \(I_B\) 仅与电阻 \(R_B\) 和 M12、M13 的尺寸有关,不受电源电压的影响。 \[ R_B = \frac{2}{\sqrt{2\mu C_{ox}(W/L)_{12}I_B}}(\sqrt{\frac{(W/L)_{12}}{(W/L)_{13}}}-1) \] 由 \(\sqrt{2\mu C_{ox}(W/L)_{12}I_B} = g_{m12}\) 以及上式可以得到: \[ g_{m12}=\frac{2}{R_B}(\sqrt{\frac{(W/L)_{12}}{(W/L)_{13}}}-1)^2 \] 可以看出,\(gm_{12}\) 仅由 \(R_B\) 以及 M12 与 M13 的器件比例而决定。若取 \((W/L)_{12}=4 (W/L)_{13}\) 则可以得到: \[ g_{m12} = \frac{2}{R_B} \]
\[ g_{m13} = \frac{1}{R_B} \]
指标分析
电路设计
设计指标
| 设计指标 | 带宽最大化 |
|---|---|
| 管子长度 | \(\geq 0.8 \mu m\) |
| 管子宽度 | \(\geq 2\mu m\) |
| 面积 | \(\leq 20000 \mu m^2\) |
| 负载电容 | \(=3pF\) |
| 共模输入电压 | 固定在 (VDD+VSS)/2 |
| 输出动态范围 | [0.1(VDD-VSS), 0.9(VDD-VSS)] |
| 静态功耗 | \(\leq 2mW\) |
| 开环直流增益 | \(\geq 80dB\) |
| 单位增益带宽 | Maximize |
| 相位裕度 | \(\geq 60 degree\) |
| 转换速率 | \(\geq 30V/\mu s\) |
| 共模抑制比 | \(\geq 60dB\) |
| 负电源抑制比 | \(\geq 80dB\) |
| 等效输入噪声 | \(\leq 300nV/Hz@1KHz\) |
约束
\[ W_1 = W_2,L_1=L_2;W_3=W_4,L_3=L_4 \]
\[ \frac{(W/L)_{3,4}}{(W/L)_{6}} = \frac{\frac{1}{2}(W/L)_{5}}{(W/L)_{7}} \]
\[ (W/L)_{8}=(W/L)_{9},(W/L)_{10}=(W/L)_{11} \]
\[ (W/L)_{12}=4(W/L)_{13} \]
\[ (k_1+k_2+2)I_{DS8}\leq 400\mu A \]
单管匹配
当晶体管工作在饱和区时,实际上的设计参数只有 \((W/L),I_{DS},V_{DSAT}\),确定了这三个变量中的两个就可以决定第三个量。在本设计中,确定晶体管的电流和过驱动电压就可以得到需要的宽长比。
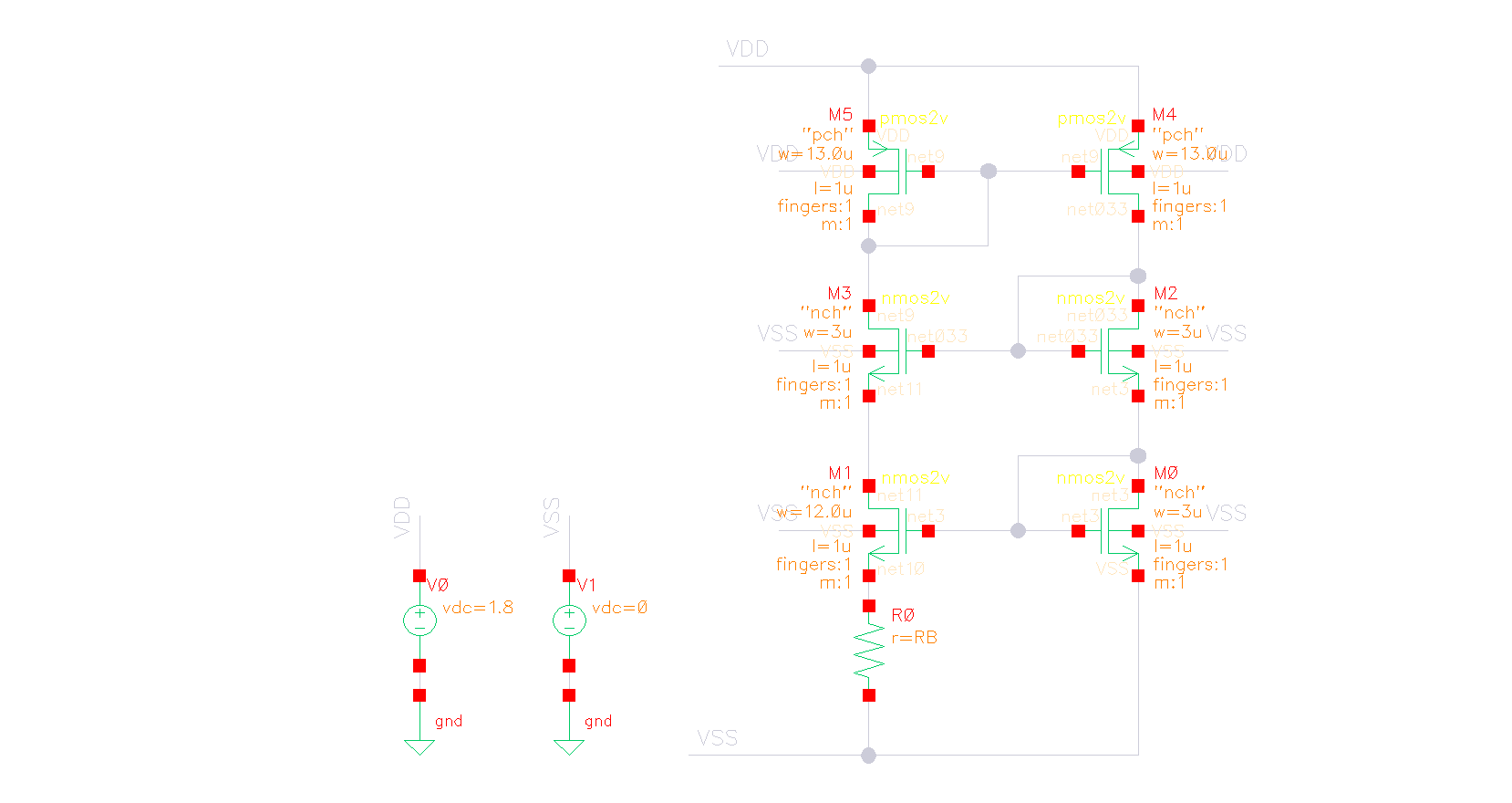
如上图所示,首先单独搭建电流镜部分。
当 \(I_{DS} = 10\mu A\) 时,扫描 W,得到在不同 \(W/L\) 下 \(V_{DSAT}\) 的值。
PMOS
| \(V_{DSAT}\) | \(W/L\) |
|---|---|
| 100m | 35 |
| 125m | 20 |
| 150m | 13 |
| 175m | 9 |
| 200m | 7 |
| 250m | 4 |
| 300m | 3 |
NMOS
| \(V_{DSAT}\) | \(W/L\) |
|---|---|
| 100m | 8.9 |
| 125m | 4.8 |
| 150m | 3 |
| 175m | 2.1 |
| 250m | 1 |
| 200m | 1.6 |
可以看到在相同的过驱动电压下,\((W/L)_p/(W/L)_n \approx 13/3\),为了保证良好的匹配性,所有位于饱和区的晶体管取相同的过驱动电压。
设计步骤
先取 \(C_c\) 为 1pF;
取 \(V_{DSAT} = 150mV\);
取 \(I_{DS8} = 10 \mu A, I_{DS5}=120\mu A, I_{DS7} = 240\mu A\);
确定晶体管参数,过驱动电压定为 150mV:
晶体管 倍数 W/L M13 1n 3/1 M12 4n 12/1 M10, M11 1n 3/11 M8, M9 1p 13/1 M5 12p 156/1 M1, M2 6p 78/1 M3, M4 6n 18/1 M7 24p 312/1 M6 24n 72/1 M14 10/1
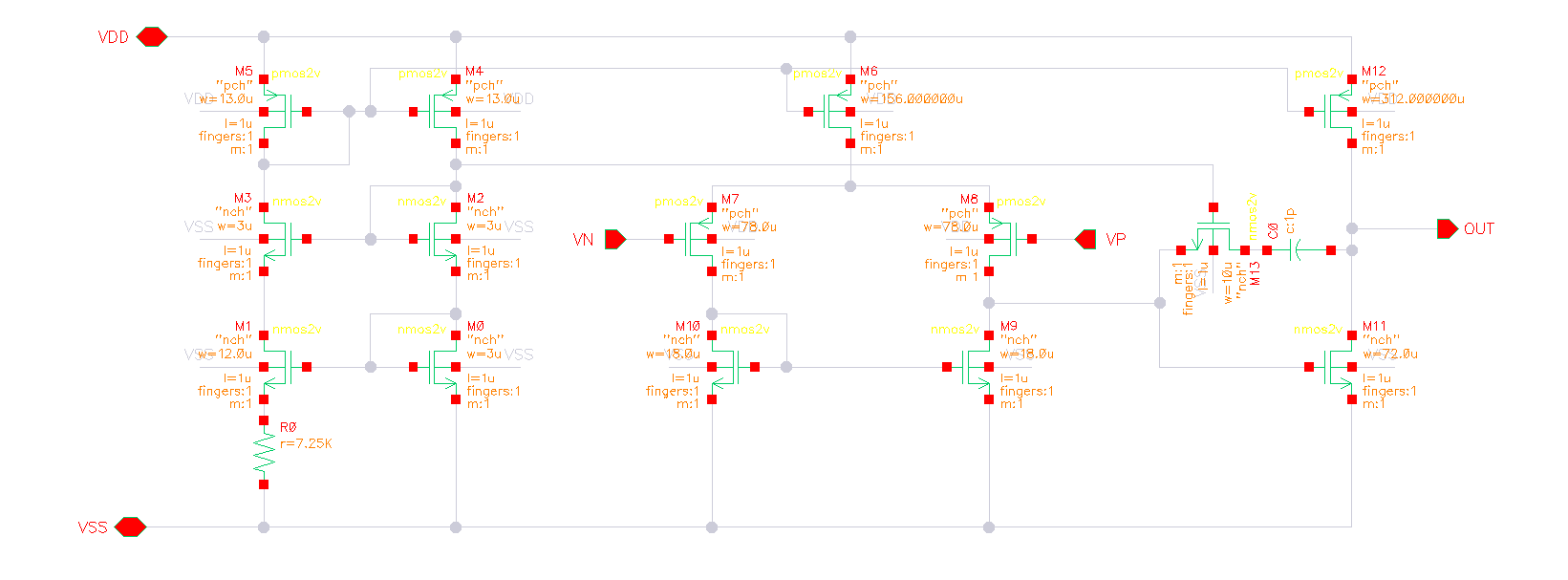
cadence 仿真
AC

通过 AC 仿真可以得到 GBW 大约为 113MHz,在单位带宽增益处,相移达到了 127°,表明相位裕度为 53°,不能满足大于 60° 的要求,因此调整米勒电容 Cc 为 1.5pF,再次仿真,得到GBW 为113MHz,相位裕度为 63°,满足要求。

噪声仿真
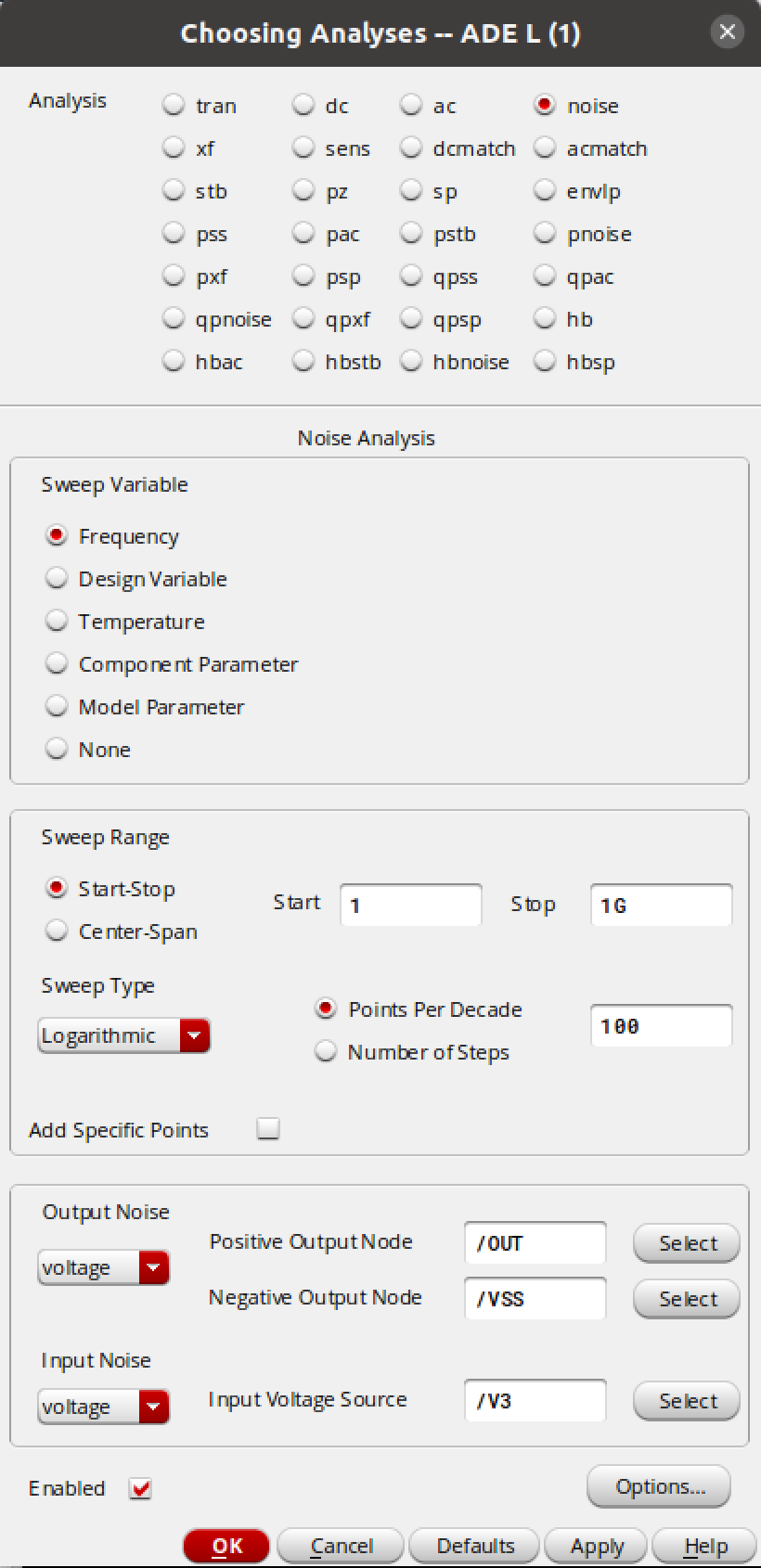
接下来仿真噪声,依照上图设置参数。其中,最下面 Positive Output Node 一栏,可点击 Select 按钮后,在电路图中选择输出节点;而 Negative Output Node 一栏则选地,若不选,则也会默认为地;Input Voltage Source 选择输入差分信号的电压源。结果选择等效输入噪声,如下:
其他指标仿真
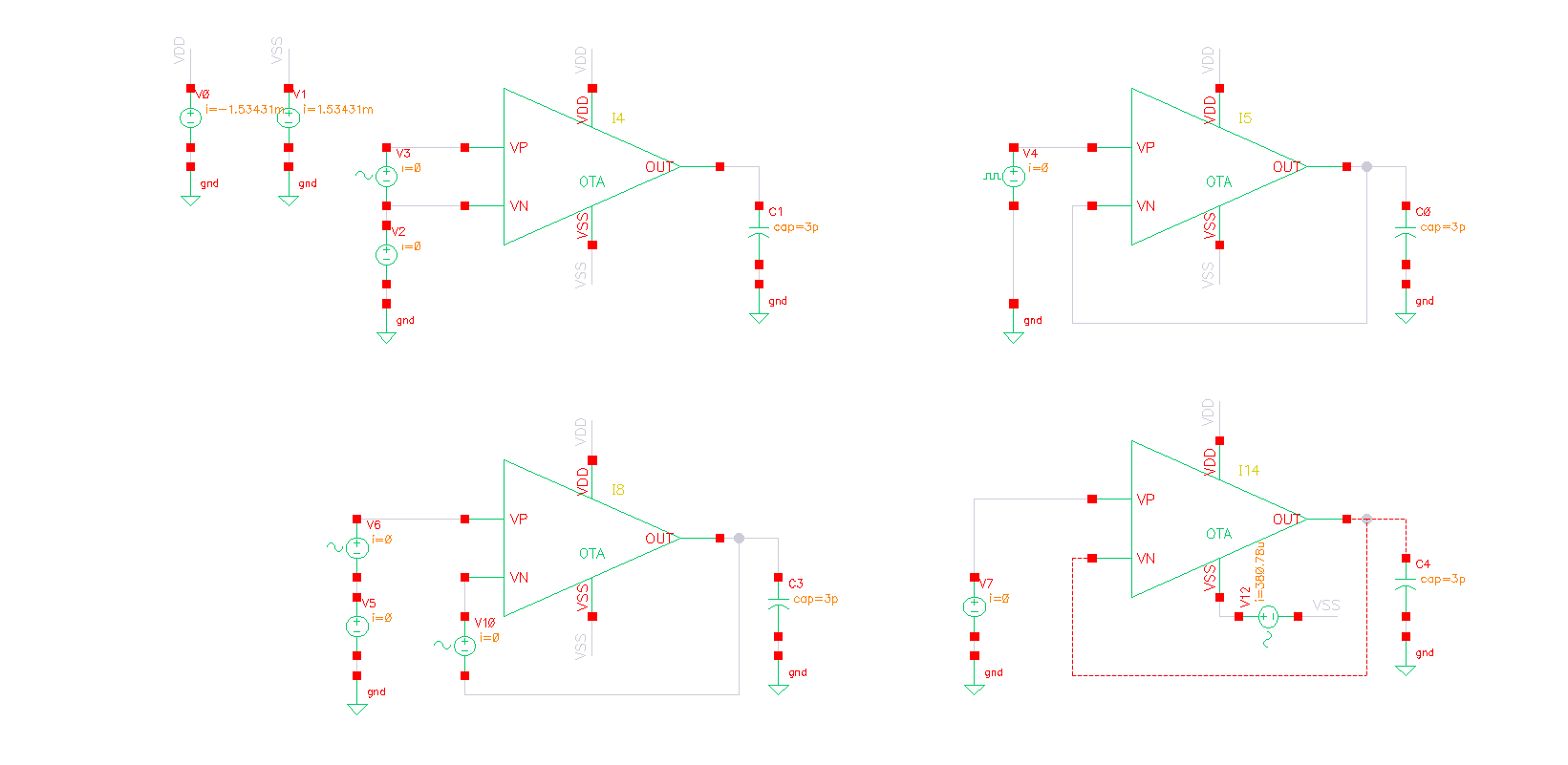
SR、CMRR 和 nPSRR,仿真如上图所示。
SR (压摆率)

其中 SR 仿真中信号源使用
vpulse,设置如上图所示。仿真时使用 tran
仿真,仿真后输出波形。
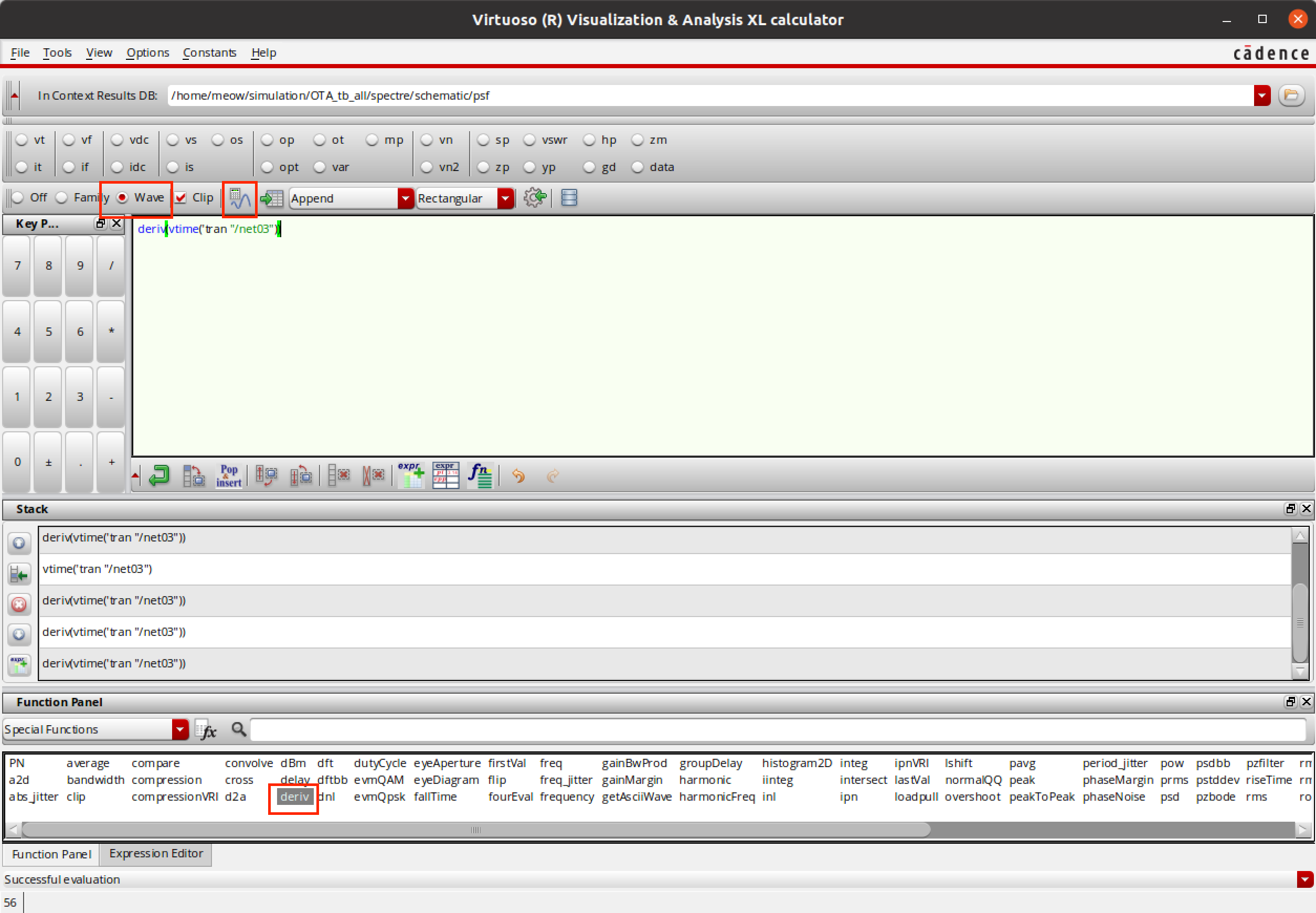
由于 SR 是电压相对于时间的导数,可以使用计算器来得到一个更直观的 SR。 设置如上图所示。SR 的结果如下图所示。

CMRR (共模抑制比)
定义为差模增益与差模输入为0时共模到输出的增益比值。物理意义即衡量共模输入转换到等效差模输入的大小。
使用两个信号源分别加载于被测放大器的同相、反相输入端,由于放大器的差模增益远远大于共模增益,因此 CMRR 可以近似为 \(V_{CM}/V_{out}\)。 \[ V_{out} = A_{DM}(V_P-V_N) + A_{CM} \] \[ V_P= V_{CM},\ \ V_N = V_{out} + V_{CM}, \ \ V_{CM} = 1 \] \[ \frac{V_{out}}{V_{CM}} = \frac{A_{CM}}{A_{DM}+1}\approx\frac{A_{CM}}{A_{DM}}=\frac{1}{CMRR} \]

电源抑制比 (PSRR)
在负电源上叠加 1V 交流电压,输出端接到负输入端,正输入端接 VDD/2 的直流电源。

仿真结果
| 设计指标 | 带宽最大化 | 仿真结果 |
|---|---|---|
| 静态功耗 | \(\leq 2mW\) | \(377\mu A\times 1.8V\) |
| 开环直流增益 | \(\geq 80dB\) | 83 dB |
| 单位增益带宽 | Maximize | 113 MHz |
| 相位裕度 | \(\geq 60 degree\) | 63 degree |
| 转换速率 | \(\geq 30V/\mu s\) | \(40 V/\mu s\) |
| 共模抑制比 | \(\geq 60dB\) | 69 dB |
| 负电源抑制比 | \(\geq 80dB\) | 89 dB |
| 等效输入噪声 | \(\leq 300nV/Hz@1KHz\) | \(91.6nV/Hz@1KHz\) |
Reference
[1] 复旦大学模拟电路二级运放实例
[2] 两级运算放大器设计笔记
[4] 运放仿真方法整理
