C-V 曲线仿真
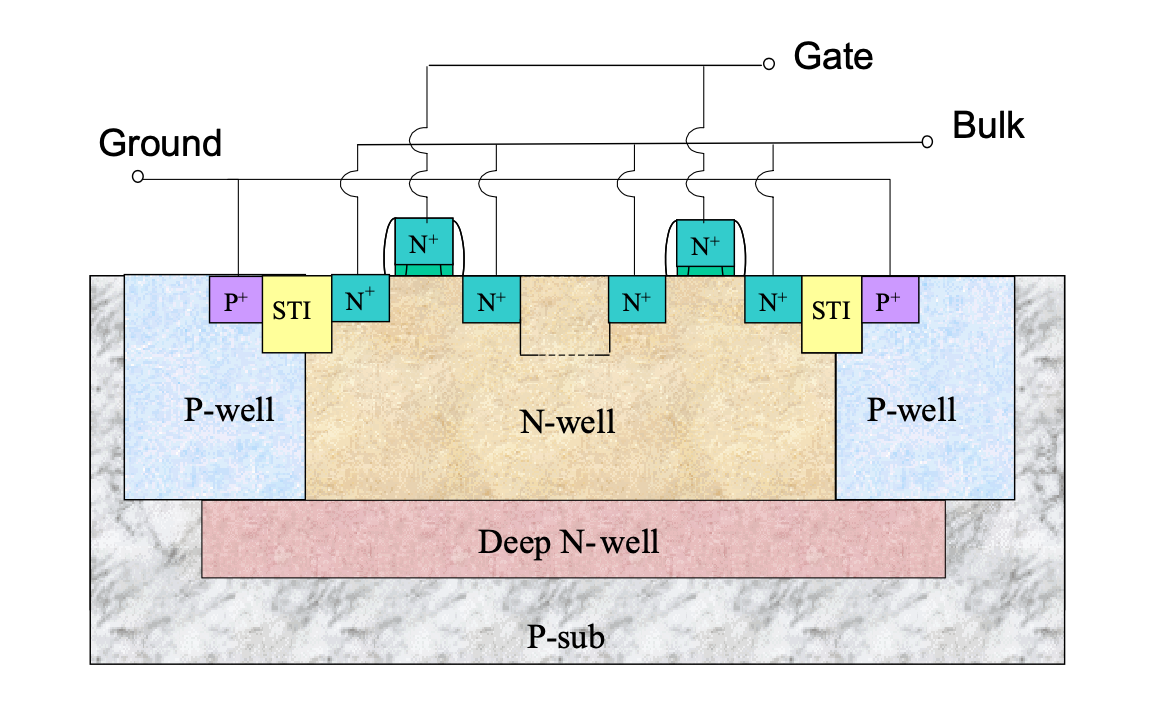
通过 S 参数仿真的方法来得到变容二极管的 C-V 曲线。变容二极管使用的是 tsmc65 工艺中的 moscap_rf_nw,其横切面的示意图如上图所示。其中 Ground 端作为控制电压的接入端,Bulk 接地,Gate 端接在电路中,最后的电容是 Gate 和 Bulk 之间的电容。该种接线方法为累积型 MOS 可变电容 (Accumulation NMOS Varactor)。
其等效电路模型如下图所示:(下图的 Gnode 端应该就是上图的 Ground 端)
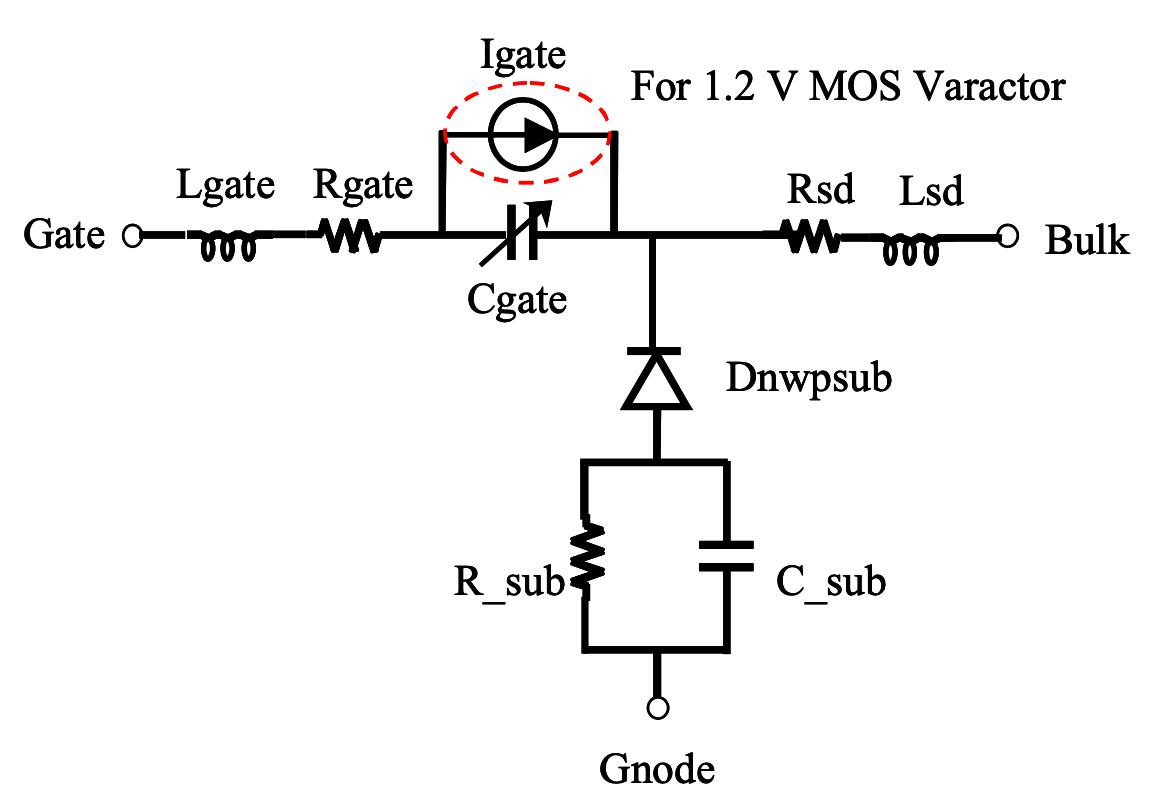
为了后续说明的方便,将模型简化为下图:
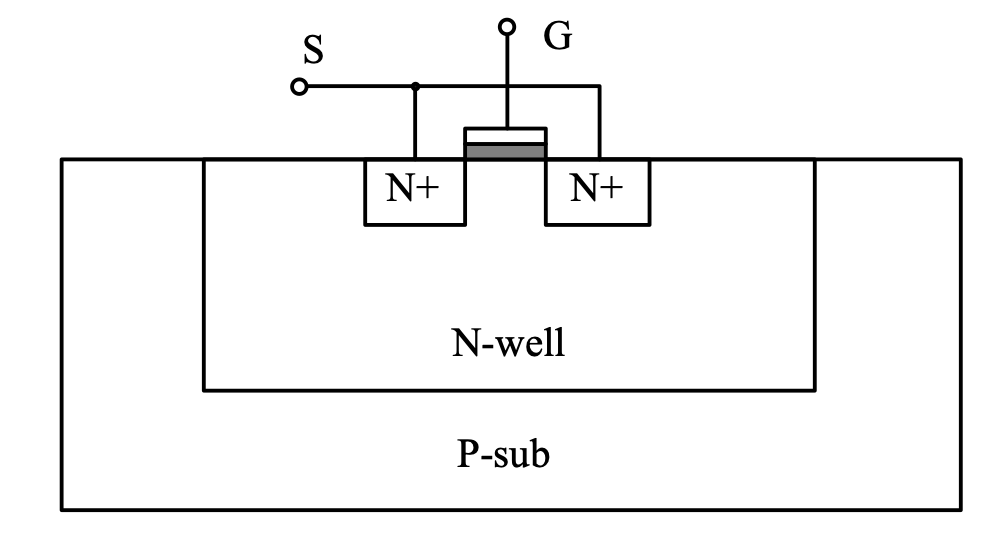
在 G 端接入一个 Port,DC 设置为 0,在 S 接入第二个 Port,DC 设置为 vctrl(此时 vctrl 相当于 \(V_{SG}\)),然后在 S 参数仿真时,扫描 vctrl,就可以获得变容二极管的 C-V 曲线。
仿真使用的原理图如下:
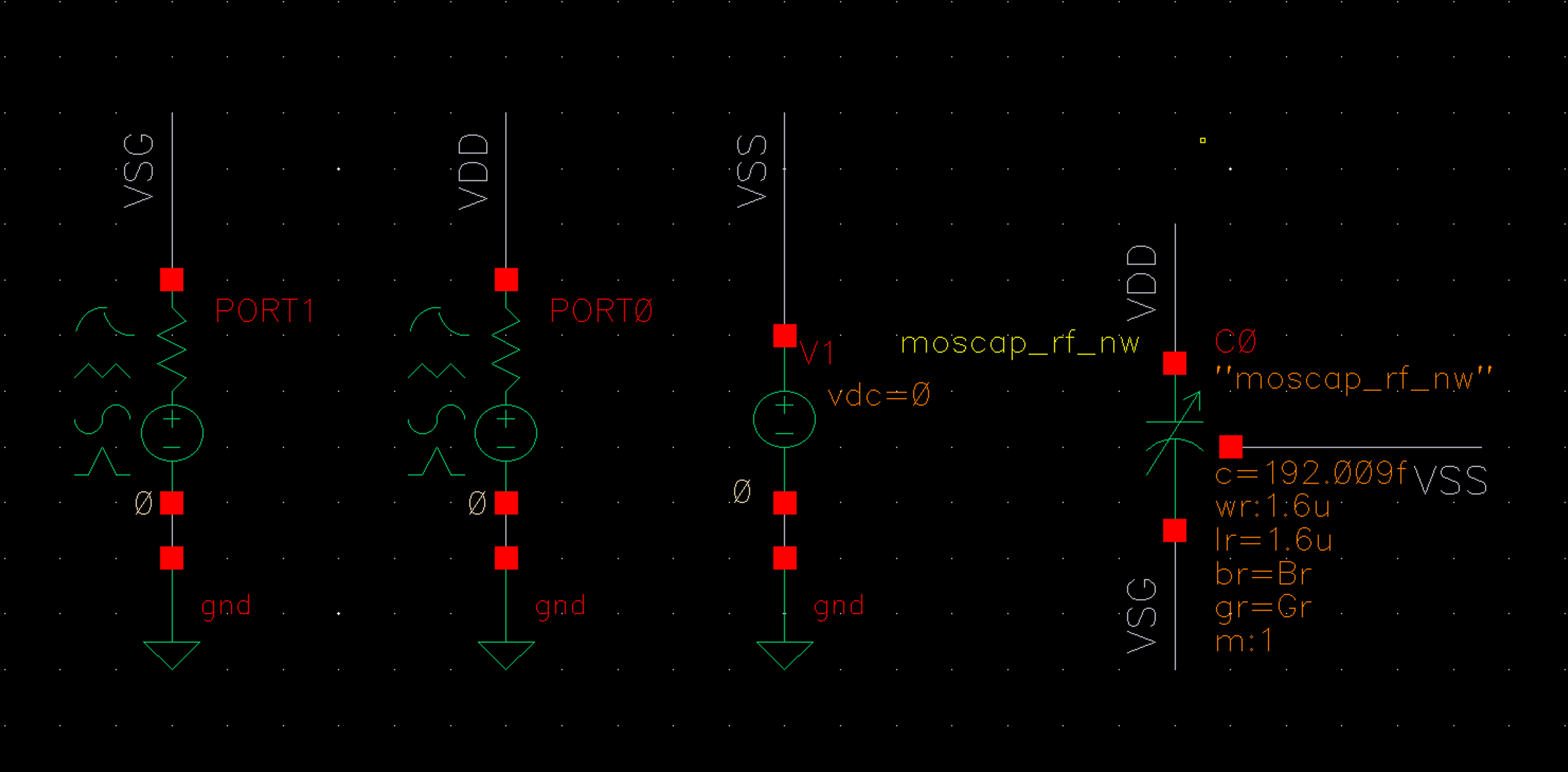
Port0 和 Port1 的设置如下:
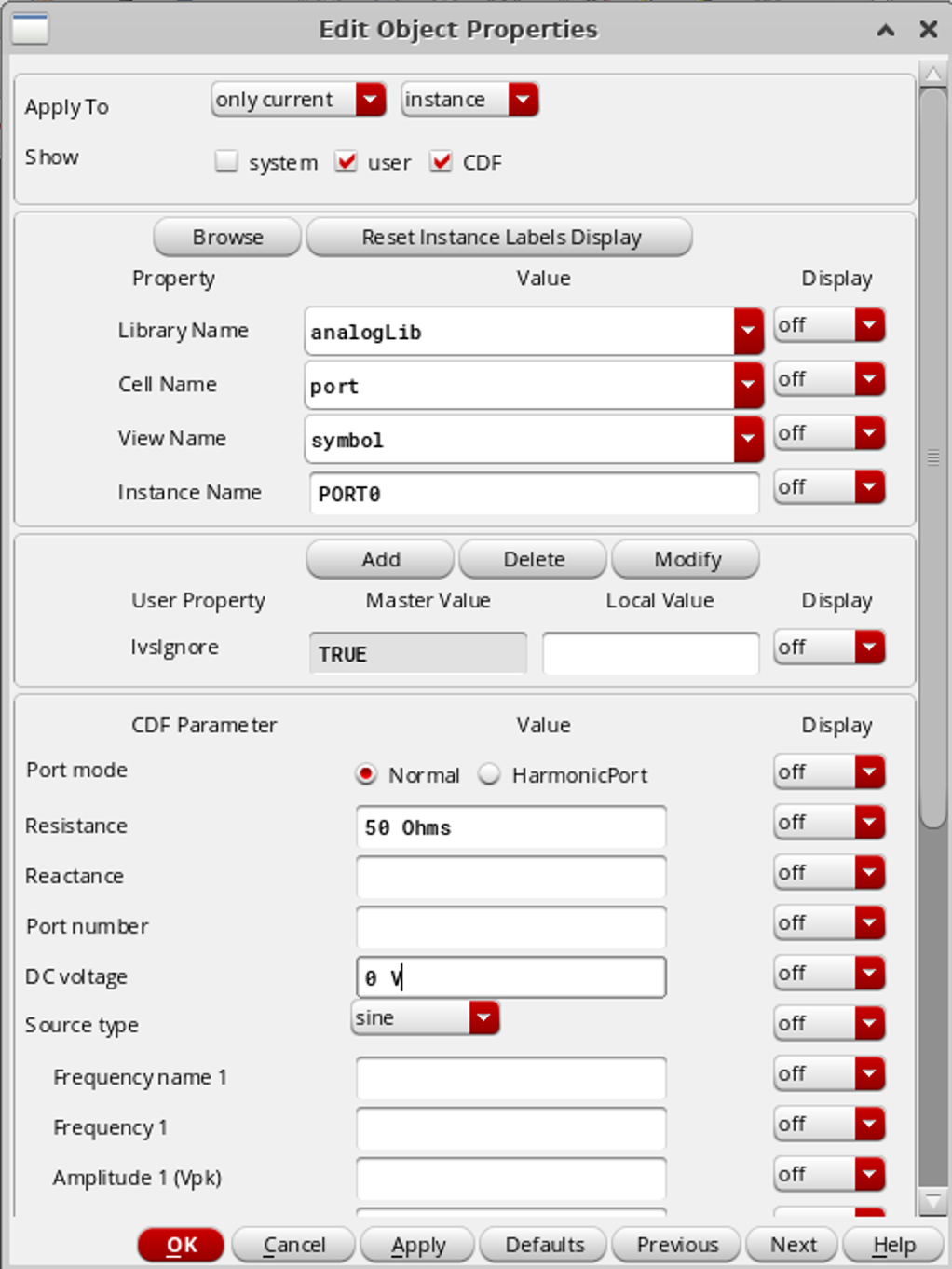
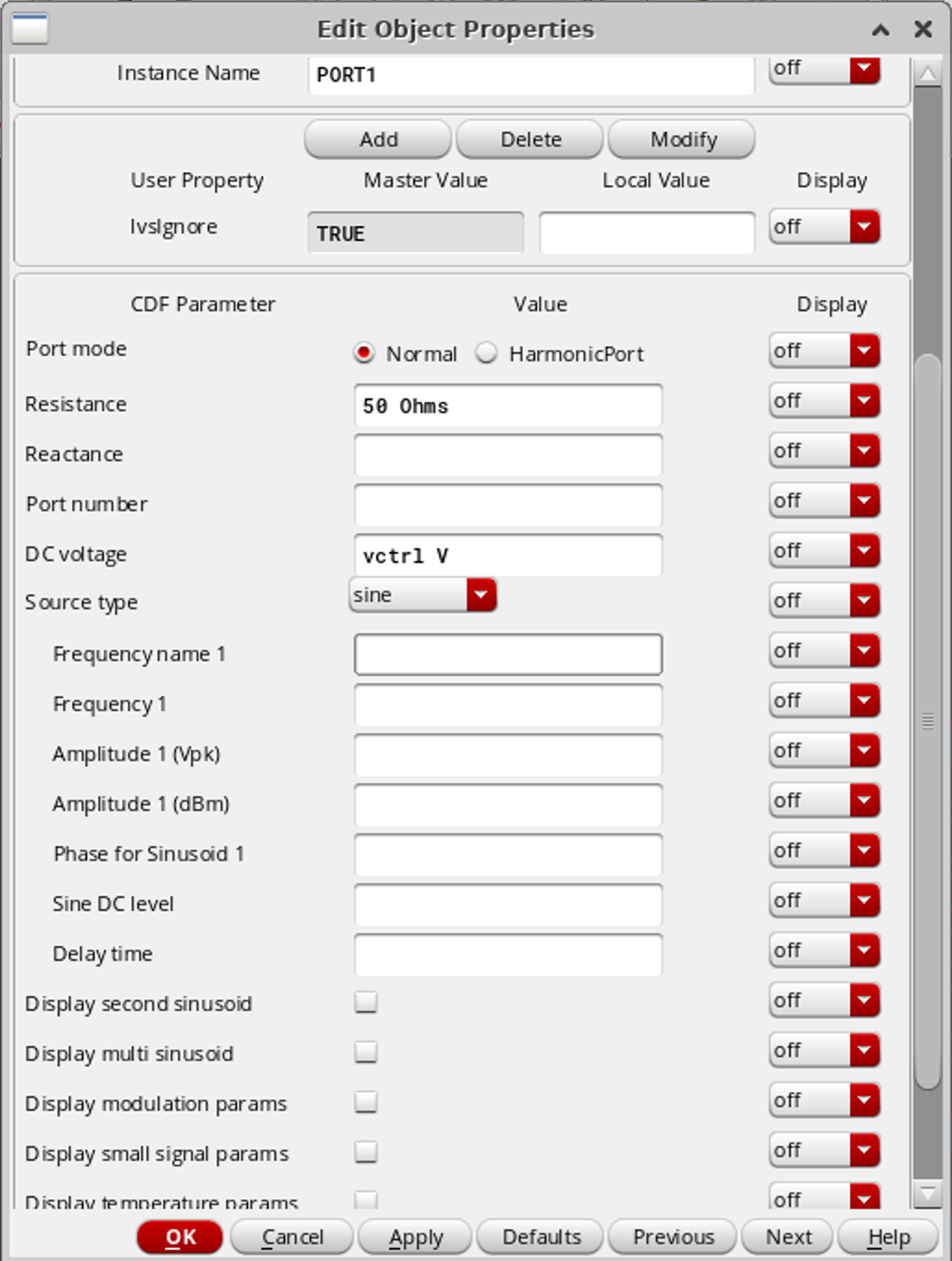
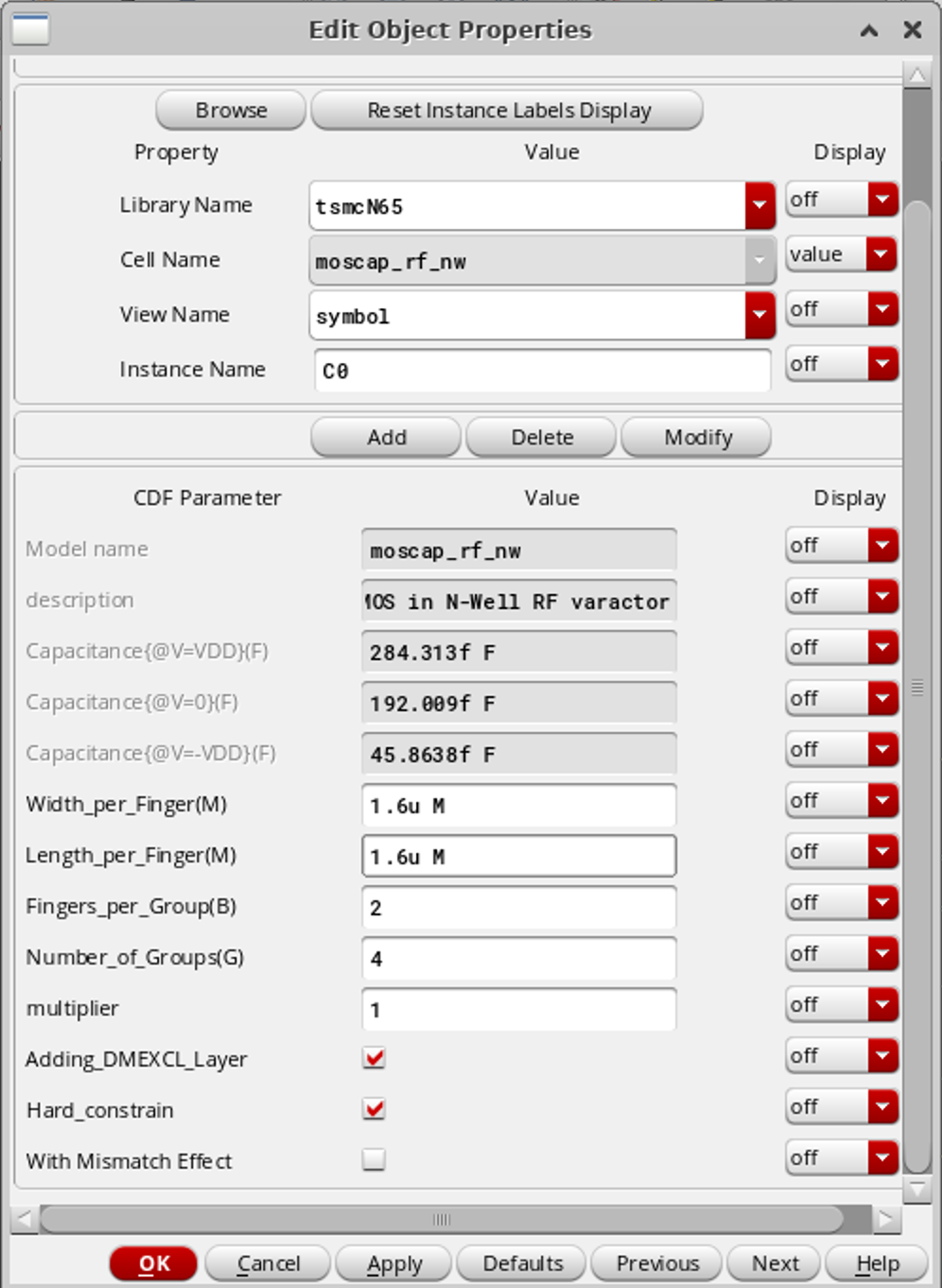
Varactor 的参数暂时设置为:WR/LR/GR/BR : 1.6μm/1.6μm/4/2,可以在元件参数设置的窗口里看到电容的 C 为:284fF(VDD)/192(0)/45(-VDD)
在 AED 中选择 sp,设置如下:
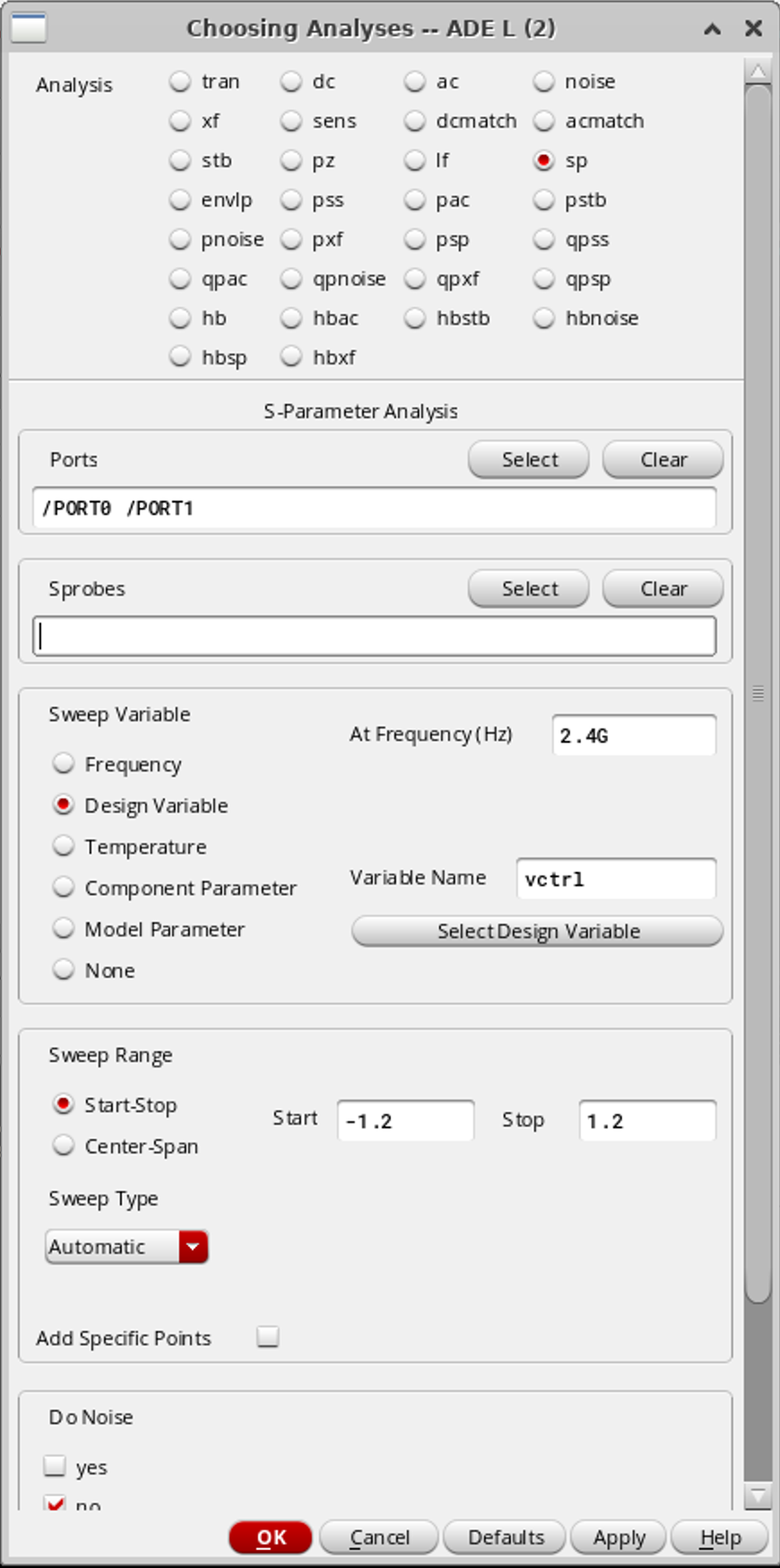
求电容的公式为:$imag(Y_{11})/(2f) $,因此在输出结果中填入如下公式:
1 | (imag(yp(1 1 ?result "sp")) /(2*pi) / 2.4e+09) |
然后运行仿真,就可以得到 C-V 曲线啦:

可以看到基本上和之前预测的电容值差不多。
线性度补偿
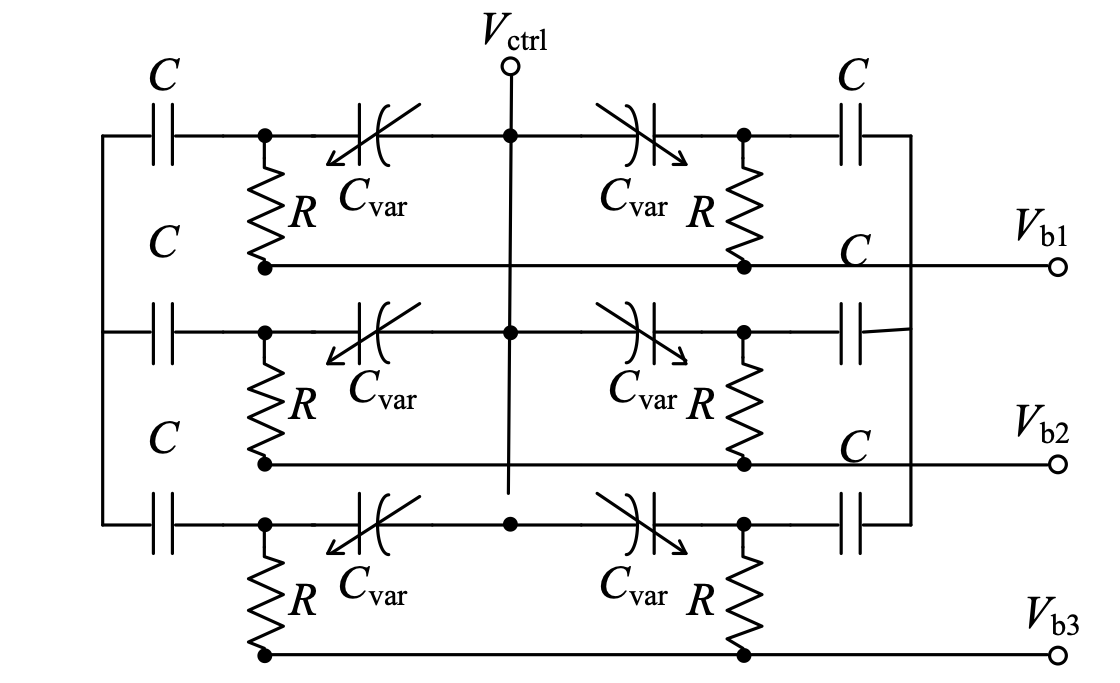
在上图的曲线中,可以观察到电容和控制电压的关系不是线性的,这将直接恶化 VCO 调谐增益的稳定性。为了提高 A-MOS 可变电容的线性度,把可变电容偏置在不同的偏置电压 Vb1、Vb2 和 Vb3 下,然后将它们并联在一起形成可变电容阵列,通过可变电容在不同偏置电压下不同的 C-V 特性的相互补偿,从而获得线性的可变电容 C-V 曲线。结构如下图所示,电阻 R 为偏置电阻,为了减小偏置电阻的热噪声对 VCO 输出相位噪声的影响,一般设置偏置电阻 R 是 LC 谐振腔并联寄生电阻的 10 倍以上。同样,电容 C 用于隔直,避免不同偏置电压对 VCO 输出偏置电压的影响,一般大小设置为可变电容的 10 倍左右。
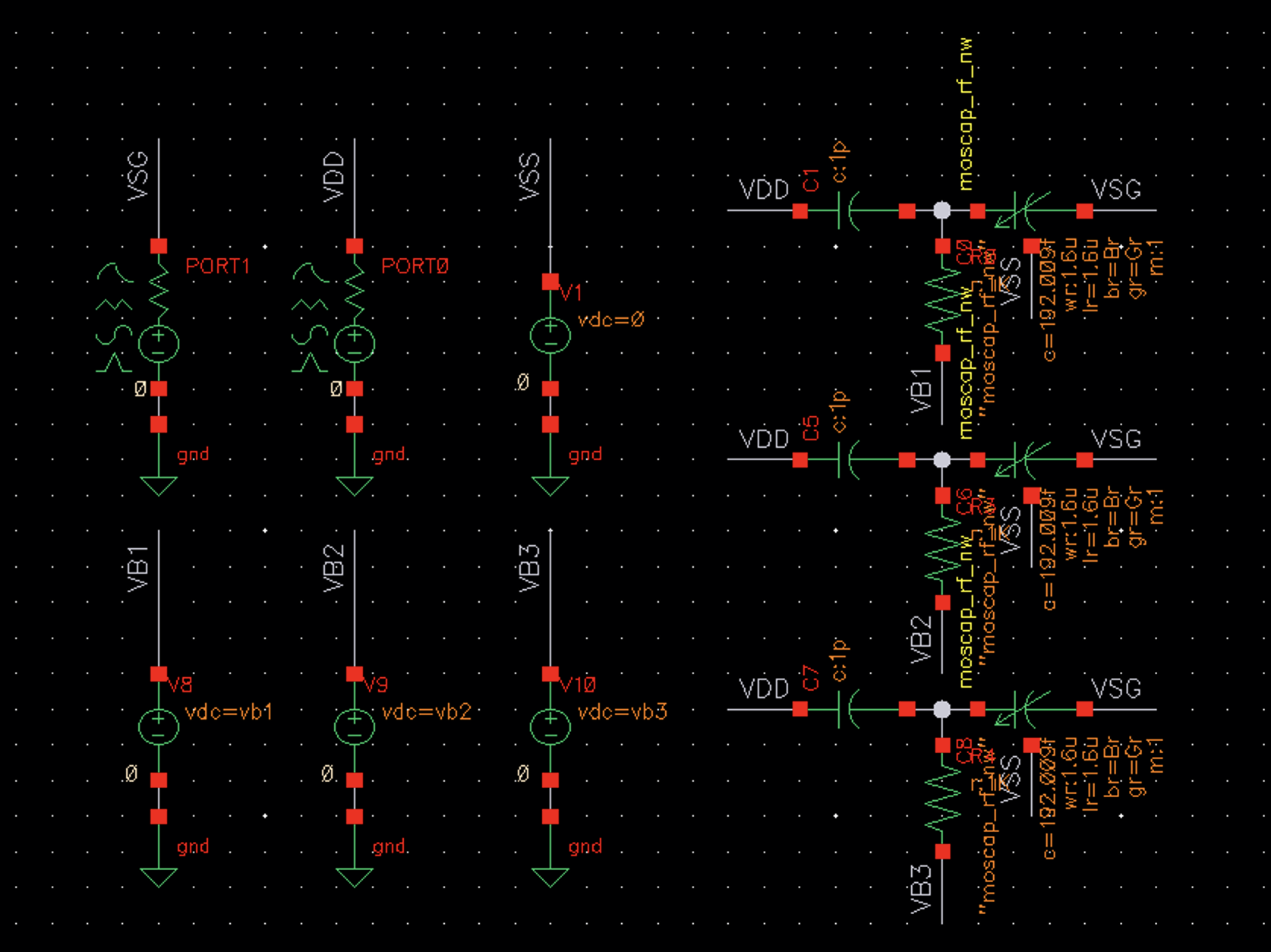
仿真使用的原理图如下:
偏置0:当 \(V_{b1},V_{b2},V_{b3}\) 都设置为 0 时,C-V
曲线如下(Kc 是 C 的变化率,公式
deriv(C))。此时相当于直接将 3 个电容并在一起。

偏置1:当 \(V_{b1},V_{b2},V_{b3}\) 分别设置为 0.3, 0.7, 1.1 时,C-V 曲线如下。相较于偏置0的设置,可以看到电容值中心值的控制电压向右移动了,同时变化率变小了,但变化范围没变。

偏置2:当 \(V_{b1},V_{b2},V_{b3}\) 分别设置为 0.5, 0.8, 1.1 时,C-V 曲线如下。相较于偏置0的设置,可以看到电容值中心值的控制电压继续向右移动,但变化率(1.5)相较于偏置0的变化率(1.2)变大了。

偏置3:当 \(V_{b1},V_{b2},V_{b3}\) 分别设置为 0.1, 0.6, 1.1 时,C-V 曲线如下。可以看到电容值中心值的控制电压想左移动,其变化率(1.0)相较于偏置0的变化率(1.2)变小了。

因此可以得到一个大概的规律:
偏置电压越分散,变化得越平坦,即线性度越高;
偏置电压的平均值越大,电容值中心值的控制电压越大。
其实可以想象三条相同变化趋势的 C-V 曲线平移后叠加,在一定范围内,平移越多,叠加后的曲线越平坦。
Reference
[1] CMOS多模多频小数频率综合器的关键技术研究与实现_廖一龙
[2] https://comp.cad.cadence.narkive.com/NqQk3p8T/about-varactor-simulation
[3] Tip of the Week: When should I use the pss/qpss Harmonic Balance vs. Shooting Newton Engine?
[4] Tip of the Week: Guidelines for simulating oscillators - phase noise simulations